알고리즘

harugi7 1개월 전

*이 내용은 인프런 그림으로 쉽게 배우는 자료구조와 알고리즘 (기본편)을 수강하며 정리한 내용입니다.

 

 재귀(recursion)

재귀는 어떠한 것을 정의할 때 자기 자신을 참조하는 것을 뜻해. 그러므로 재귀함수는 탈출 조건, 즉 기저 조건이 반드시 있어야 해.

콜스택

함수가 호출되면서 올라가는 메모리 영역으로 스택이라고도 불러. FILO의 특징을 띄고있어.

상향식 계산 vs 하향식 계산

image

  • 재귀를 이용한 상향식 계산

    • 하지만 재귀는 하향식 계산일 때 위력을 발휘해!

image

하노이 탑

image

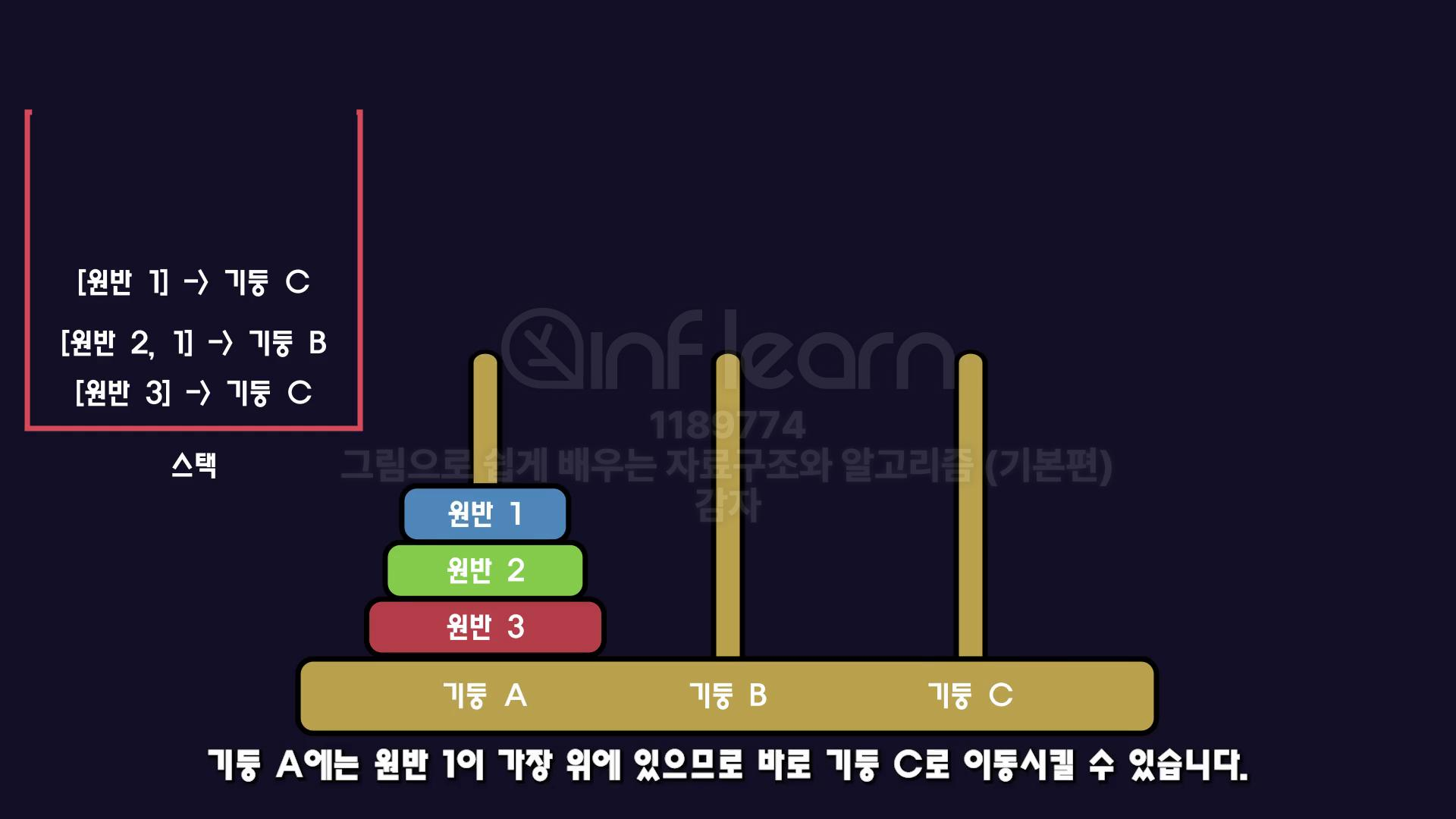
function hanoi(count, from, to, temp){
    if(count == 0) return;
    hanoi(count - 1, from, temp, to);
    console.log(`${count} ${from} -> ${to}`);
    hanoi(count - 1, temp, to, from);
}

hanoi(3, "A", "C", "B");

 

정렬

버블정렬

데이터를 옆 데이터와 비교하는 정렬이야.

function BubbleSort(arr){
    for(let i = 0; i < arr.length - 1; i++){
        for(let j = 0; j < (arr.length - i - 1); j++){
            if(arr[j] > arr[j + 1]){ // j, j+1 비교
                let temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

  • 성능

image위와 같으므로 빅 오는 O(n**2)이 돼!

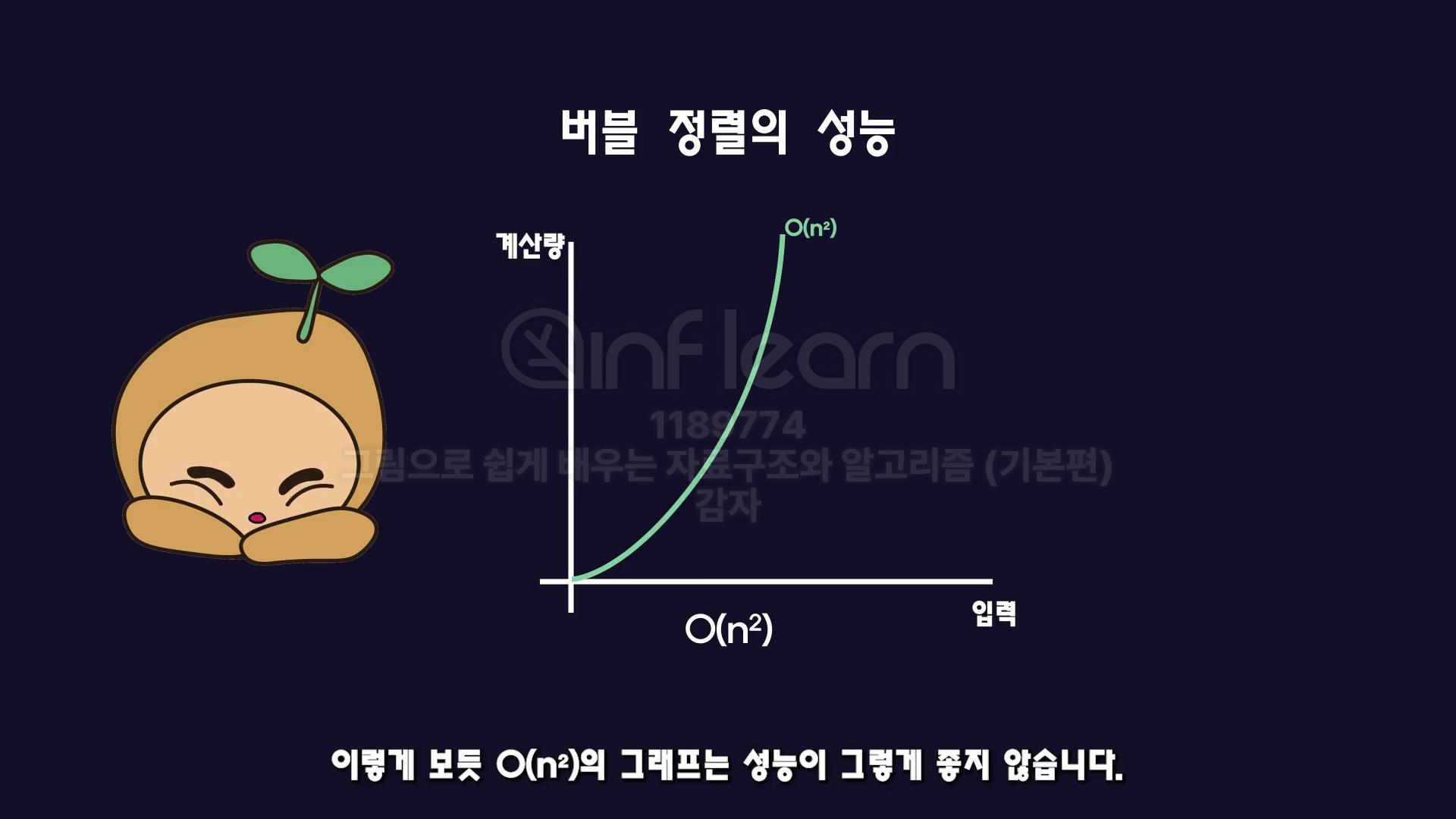image성능이 중요한 시스템을 만드려면 버블 정렬은 어려울 수도 있어...

  • 장점 : 이해와 구현이 간단함

  • 단점 : 성능이 좋지 않음

선택 정렬

배열의 정렬되지 않은 영역의 첫 번째 원소를 시작으로 마지막 원소까지 비교 후 가장 작은 값을 첫 번째 뭔소로 가져오는 정렬이야.

function SelectionSort(arr){
    for(let i = 0; i < arr.length - 1; i++){
        let minValueIndex = i;

        for(let j = i + 1; j < arr.length; j++){ // 가장 작은 index 찾기
            if(arr[j] < arr[minValueIndex]){
                minValueIndex = j;
            }
        }

        let temp = arr[i];
        arr[i] = arr[minValueIndex];
        arr[minValueIndex] = temp;
    }
}

  • 성능

     

    image버블정렬과 동일해! 즉 선택 정렬의 정렬도 O(n**2)이야.

  • 장점 : 이해와 구현이 간단함

  • 단점 : 성능이 좋지 않음

     

     

    삽입정렬

    정렬되지 않은 영역의 데이터를 정렬된 영역에 끼워 넣는 정렬방식이야.

     

    정렬된 영역을 뒤에서부터 역순으로 비교해.

function InsertionSort(arr){
    for(let i = 1; i < arr.length; i++){
        let insertingData = arr[i];
        let j;
        for(j = i - 1; j >= 0; j--){
            if(arr[j] > insertingData){
                arr[j + 1] = arr[j];
            }else{
                break;
            }
        }
        arr[j + 1] = insertingData;
    }
} 

  • 성능 :

    위 정렬들과 마찬가지고 O(n**2)이야.

  • 장점 : 이해와 구현이 간단함

  • 단점 : 성능이 좋지 않음

병합정렬

분할 정복 알고리즘이야.

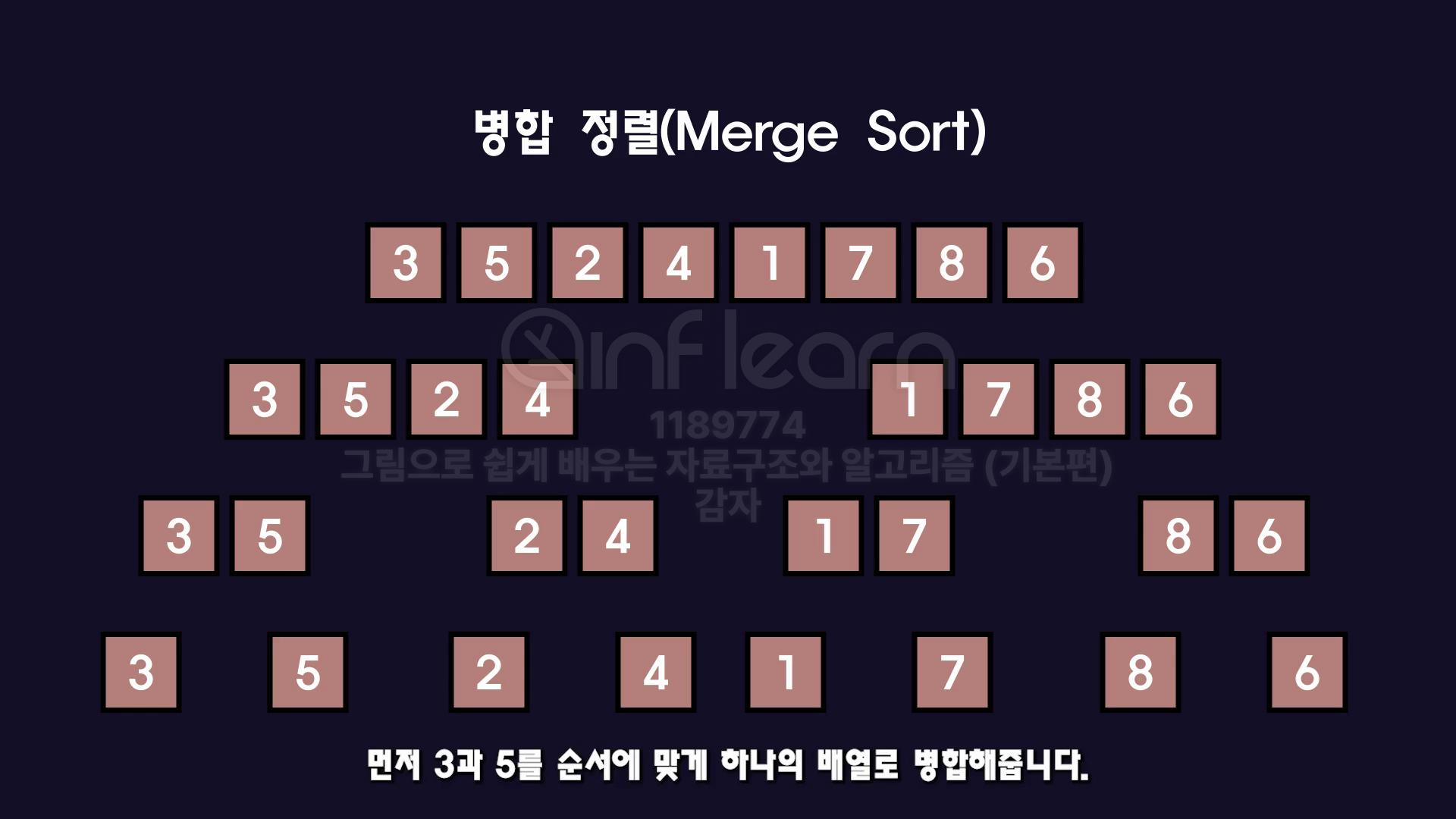image숫자 하나가 들어있는 배열로 만들어주었으면 두 배열을 순서에 맞게 정렬한 후 두개의 숫자가 들어있는 배열 하나로 만들어 줘.

image이런식으로~

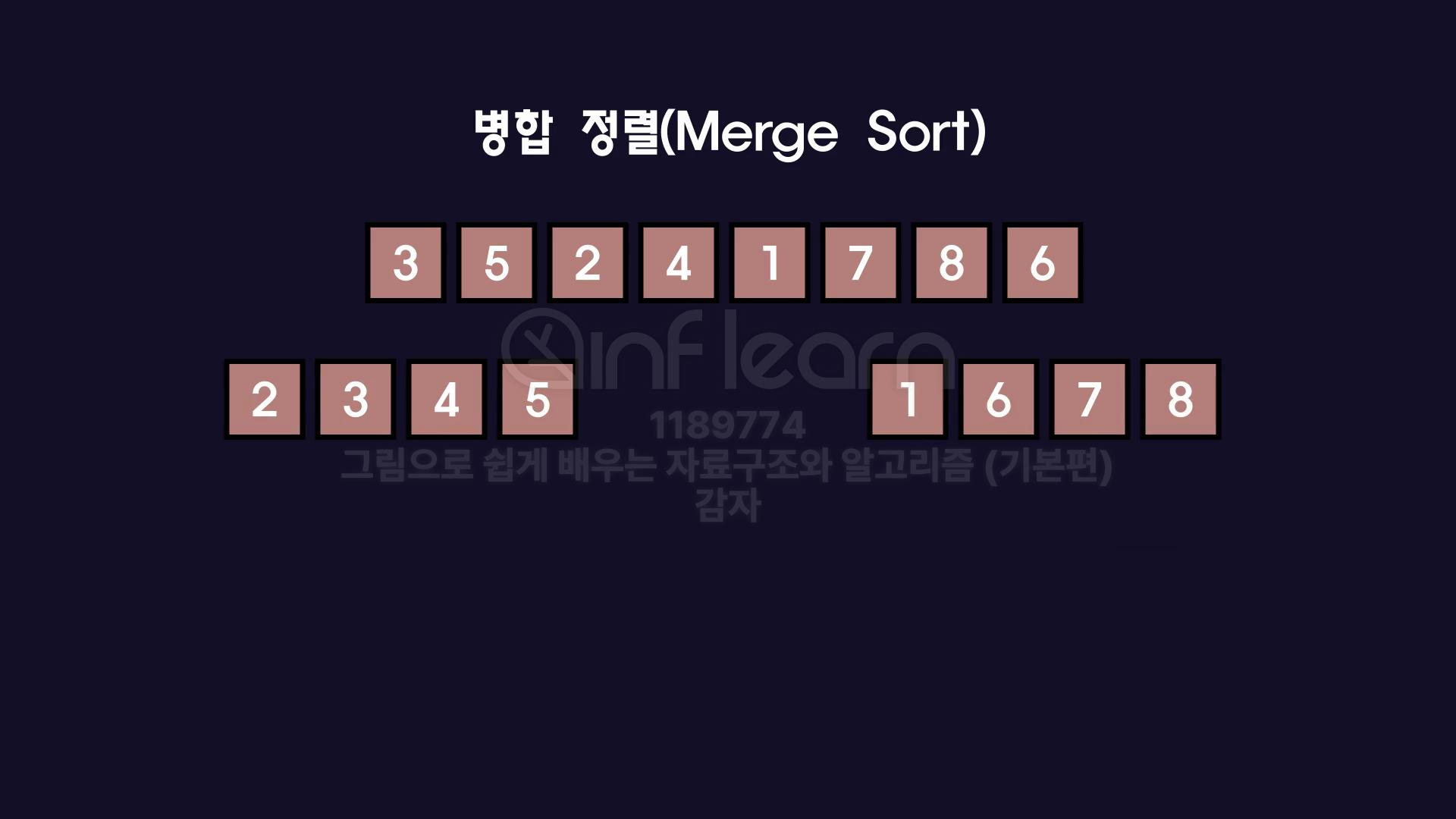image같은 방식으로 이렇게 배열해주면 돼.

function MergeSort(arr, leftIndex, rightIndex){
    if(leftIndex < rightIndex){
        let midIndex = parseInt((leftIndex + rightIndex) / 2);
        MergeSort(arr, leftIndex, midIndex);
        MergeSort(arr, midIndex + 1, rightIndex);
        Merge(arr, leftIndex, midIndex, rightIndex);
    }
}

function Merge(arr, leftIndex, midIndex, rightIndex){
    let leftAreaIndex = leftIndex;
    let rightAreaIndex = midIndex + 1;

    let tempArr = [];
    tempArr.length = rightIndex + 1;
    tempArr.fill(0, 0, rightIndex + 1);

    let tempArrIndex = leftIndex;
    // tempArrIndex에 정렬해주기 ( leftArea 혹은 rightArea 둘 중 하나 정렬.)
    while(leftAreaIndex <= midIndex && rightAreaIndex <= rightIndex){ // 왼쪽 영역과 오른쪽 영역이 정렬되지 않을 동안
        if(arr[leftAreaIndex] <= arr[rightAreaIndex]){
            tempArr[tempArrIndex] = arr[leftAreaIndex++];
        }else{
            tempArr[tempArrIndex] = arr[rightAreaIndex++];
        }
        tempArrIndex++;
    }

    // 남은 절반 값 넣어주기
    // 한쪽 영역이 전부 병합되었다면 나머지 영역은 정렬이 되어있다.
    if(leftAreaIndex > midIndex){
        for(let i = rightAreaIndex; i <= rightIndex; i++){
            tempArr[tempArrIndex++] = arr[i];
        }
    }else{
        for(let i = leftAreaIndex; i <= midIndex; i++){
            tempArr[tempArrIndex++] = arr[i];
        }
    }

    for(let i = leftIndex; i <= rightIndex; i++){
        arr[i] = tempArr[i];
    }
}

  • 성능

image하나의 데이터와 하나의 데이터가 하나로 합쳐질 때 비교 연산을 두 번 해.

마찬가지로 두개의 데이터와 두개의 데이터가 하나로 합쳐질 때에는 비교가 네번 이루어져.

각 단계를 거칠 때마다 영역의 수가 반으로 줄기 때문에 log(n)으로 말할 수 있어.

분할된 배열을 병합할 때는 n개의 데이터를 n번 비교하므로

n과 log(n)을 곱해서 O(nlogn)이야.

  • 장점 : 성능이 좋음

  • 단점 : 이해와 구현이 어려움

퀵정렬

병합정렬과 마찬가지고 분할 정복 알고리즘이야.

우선 pivot을 랜덤으로 설정해.

leftStartIndex는 오른쪽으로 이동하다가 피벗보다 큰 값을 만나면 멈춰.

rightStartIndex는 왼쪽으로 이동하다가 피벗보다 작은 값을 만나면 멈춰.

그리고 두 값을 swap 해.

계속 반복하다가 서로 지나치게 되면 rightStartIndex와 pivot을 swap해줘.

이렇게되면 pivot를 기준으로 왼쪽은 모두 pivot보다 작은 값이 위치하고, 오른쪽은 모두 pivot보다 큰 값이 위치하게 돼.

이를 반복하면 되는거지!

  • quickSort

function quickSort(arr, left, right){
    if(left <= right){ // 기저 조건
        let pivot = divide(arr, left, right); // 정렬된 pivot의 위치
        console.log(right);
        quickSort(arr, left, pivot - 1);
        quickSort(arr, pivot + 1, right);
    }
}

  • divide

function divide(arr, left, right){ // 정렬
    let pivot = arr[left];
    let leftStartIndex = left + 1;
    let rightStartIndex = right;

    while(leftStartIndex <= rightStartIndex){ // leftStartIndex 이동
        while(leftStartIndex <= right && pivot >= arr[leftStartIndex]){
            leftStartIndex++;
        }

        while(rightStartIndex >= (left + 1) && pivot <= arr[rightStartIndex]){ // rightStartIndex 이동
            rightStartIndex--;
        }

        if(leftStartIndex <= rightStartIndex){ // 서로 지나치지 않았다면 swap
            swap(arr, leftStartIndex, rightStartIndex);
        }
    }

    swap(arr, left, rightStartIndex); // pivot과 rightStartIndex를 swap
    return rightStartIndex;
}

  • swap

function swap(arr, index1, index2){
    let temp = arr[index1];
    arr[index1] = arr[index2];
    arr[index2] = temp;
}

 

  • 성능

데이터가 한 개가 될 떄까지 반으로 나누므로 log(n)!

이 작업을 데이터 n개만큼 반복해야하므로 n을 곱함!

image보통 최악의 pivot을 선택하는 경우는 드물기때문에 평균 성능인 nlogn으로 표시해.

퀵 정렬의 장단점은 병합 정렬과 동일해. 병합 정렬이 더 좋아보이지만 실제로 퀵 정렬이 더 좋게 평가돼.

 

 동적 프로그래밍

메모이제이션

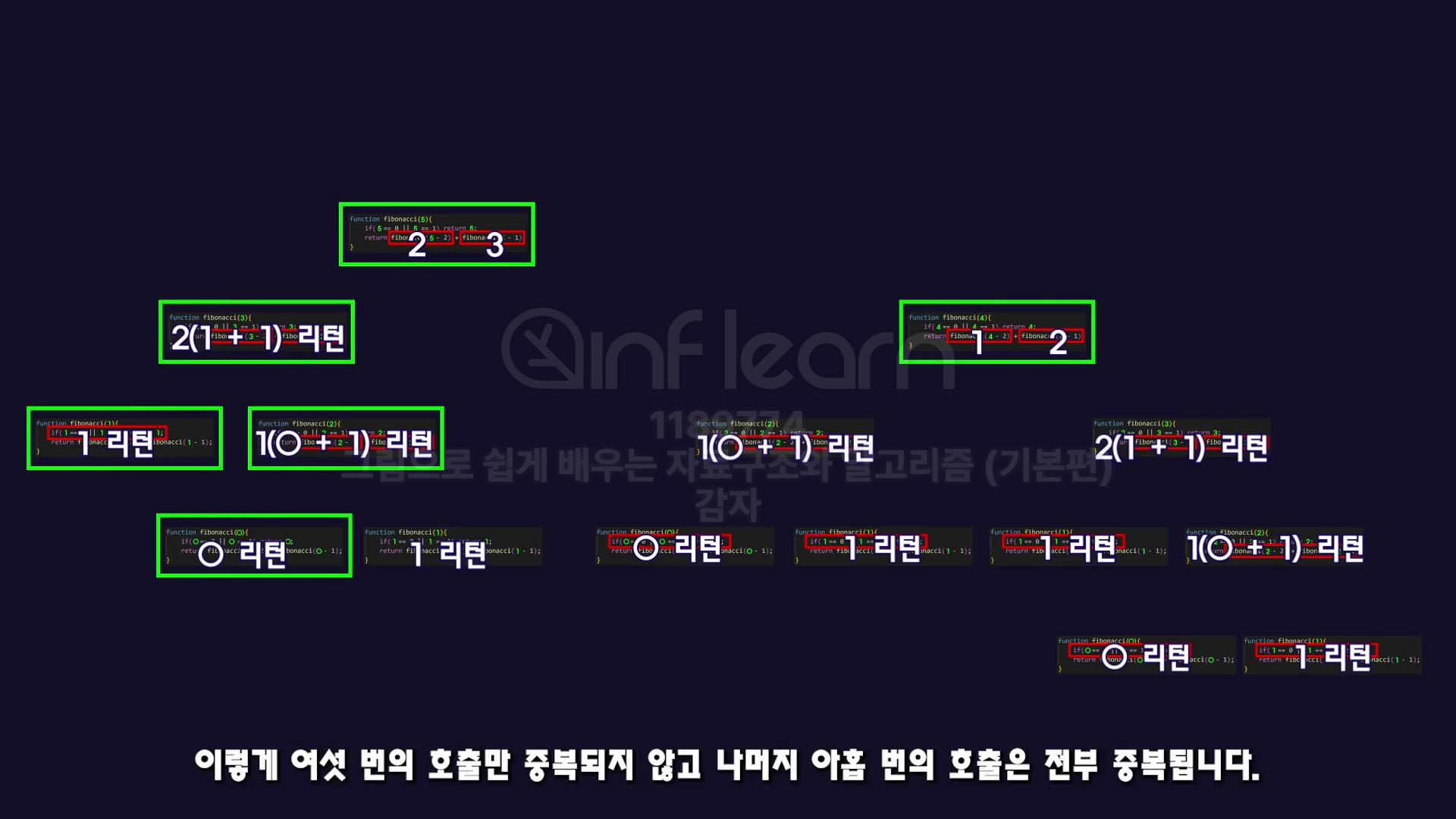image피보나치 수열을 구현할 때 재귀함수를 이용하게되면 위 사진처럼 중복되는 호출이 많아.

 그럼 중복되는 계산 결과를 저장하고, 같은 계산이 필요할 때 저장도니 결과를 사용하면 더 좋겠지?

그렇게되면 함수의 호출 수가 줄어들게되고 성능이 향상될거야.

이를 메모이제이션이라고 해.

그럼 어떤 자료구조를 사용하면 될까? 바로 해시 테이블이야.

빠른 데이터 탐색, 삽입, 삭제가 가능하기 때문이지!

해시 테이블의 key로 계산하려는 값을, value로 계산 결과를 저장하면 검색을 빠르게 할 수 있을거야.

자바스크립트 객체 또한 해시테이블이므로 이를 이용하여 코드를 작성해볼게.

function fibonacci2(n, memo){
    if(n == 0 || n == 1) return n;

    if(memo[n] == null){ // 계산 결과가 없다면 저장
        memo[n] = fibonacci2(n - 2, memo) + fibonacci2(n - 1, memo);
    }

    return memo[n];
}

이러면 실행 속도가 훨씬 빨라져.

타뷸레이션

function fibonacci2(n, memo){
    if(n == 0 || n == 1) return n;

    if(memo[n] == null){
        memo[n] = fibonacci2(n - 2, memo) + fibonacci2(n - 1, memo);
    }

    return memo[n];
}

 

image

 

 

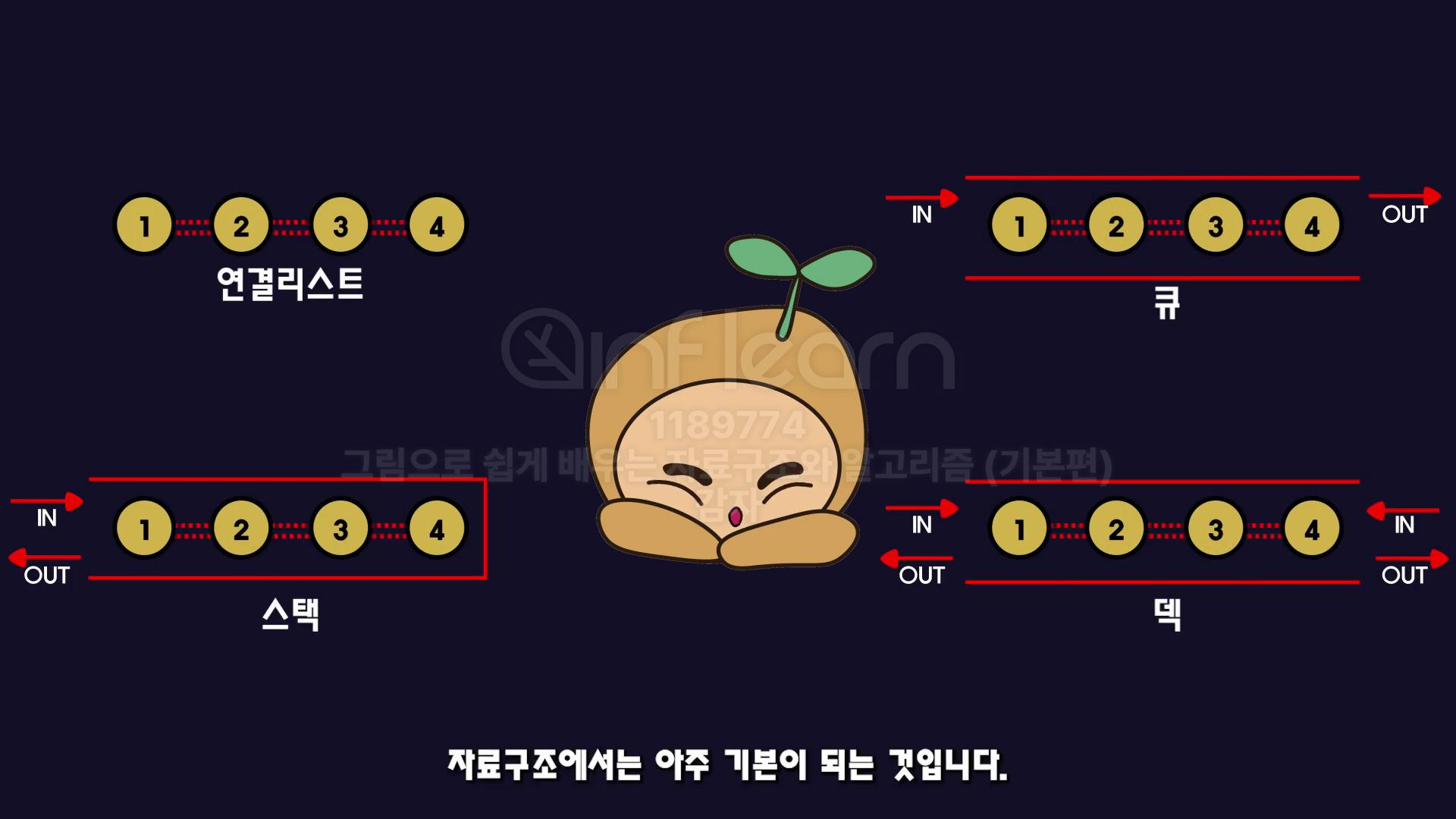
참조 : 그림으로 쉽게 배우는 자료구조와 알고리즘 (기본편)

 

  • 3주차 회고

    • 칭찬하고 싶은 점 : 기한을 지켰다 😅

    • 아쉬웠던 점 : 권장 커리큘럼을 지키지 못했다.

댓글을 작성해보세요.

채널톡 아이콘