자료구조와 알고리즘

재귀(Recursion)

재귀(Recursion)란 어떠한 것을 정의할 때 자기 자신을 참조하는 것을 뜻한다.

재귀 함수는 말 그대로 자기 자신을 계속 호출하는 함수이다. 아래의 예시를 보자.

function myFunction(number){
    console.log(number);
    myFunction(number + 1);
}

myFunction(1);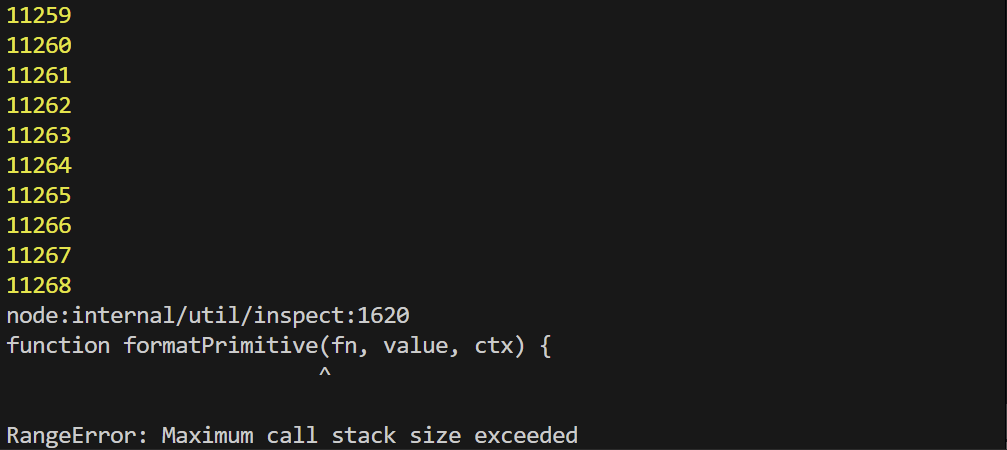

재귀 함수는 위의 결과처럼 자기 자신을 계속 호출해 메모리가 가득 찰 때까지 반복한다.

이런 재귀 함수를 쓰임새 있게 만들려면 함수를 종료하는 탈출 조건(=기저 조건)이 반드시 있어야 한다.

위의 코드에서 1~10까지의 데이터만 얻기 위해 기저 조건을 삽입 했을 때 비로소 원하는 데이터를 얻을 수 있다.

function myFunction(number){
    if(number > 10) return;
    console.log(number);
    myFunction(number + 1);
}

myFunction(1);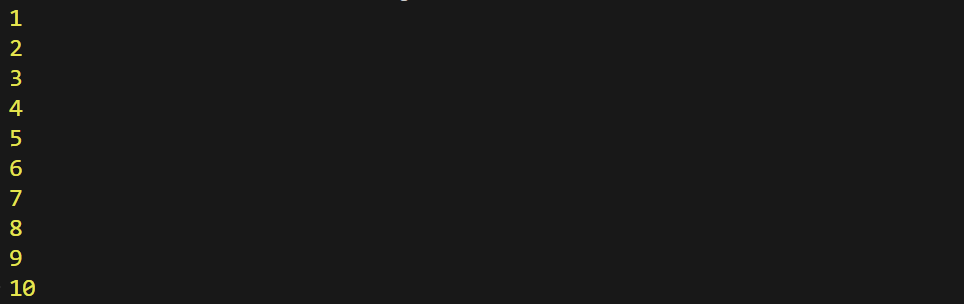

재귀 함수의 이해

콜스택

함수가 호출되면서 올라가는 메모리 영역으로, 스택으로도 부른다. 스택이 가지는 특성인 FILO(First In Last Out)를 따라 먼저 들어온 데이터가 나중에 나간다.

재귀 함수의 경우 함수 안에서 호출한 자신의 함수를 계속 스택 위로 쌓아 올리게 된다. 위의 코드를 그림으로 보면 다음과 같다. 그러므로 가장 위에 실행된 함수를 먼저 처리하고 먼저 실행한 단계 별로 내려가며 실행을 완료해 나가면 된다.

재귀적으로 생각하기

1. 반복적 실행

반복문으로 구현했을 때보다 크게 이점이 되는 부분이 없고 오히려 메모리 공간을 많이 차지해 for문보다 성능이 낮다.

2. 하향식 계산

하위 문제의 결과를 기반으로 현재 문제를 계산하는 방식인데, 이 계산 방법은 오직 재귀 함수로만 가능하며 재귀 함수를 사용하는 이유라고 할 수 있다.

배열의 합, 문자열의 길이, 지수 함수를 모두 재귀 함수를 이용해 구현 해봤는데, 이전의 문제가 이미 해결됐다고 가정하는 식으로 코드를 작성하면 좀 더 쉽게 재귀 함수를 이용할 수 있다.

하노이의 탑

재귀 함수를 배울 때 가장 기본으로 나오는 문제로, 규칙은 다음과 같다.

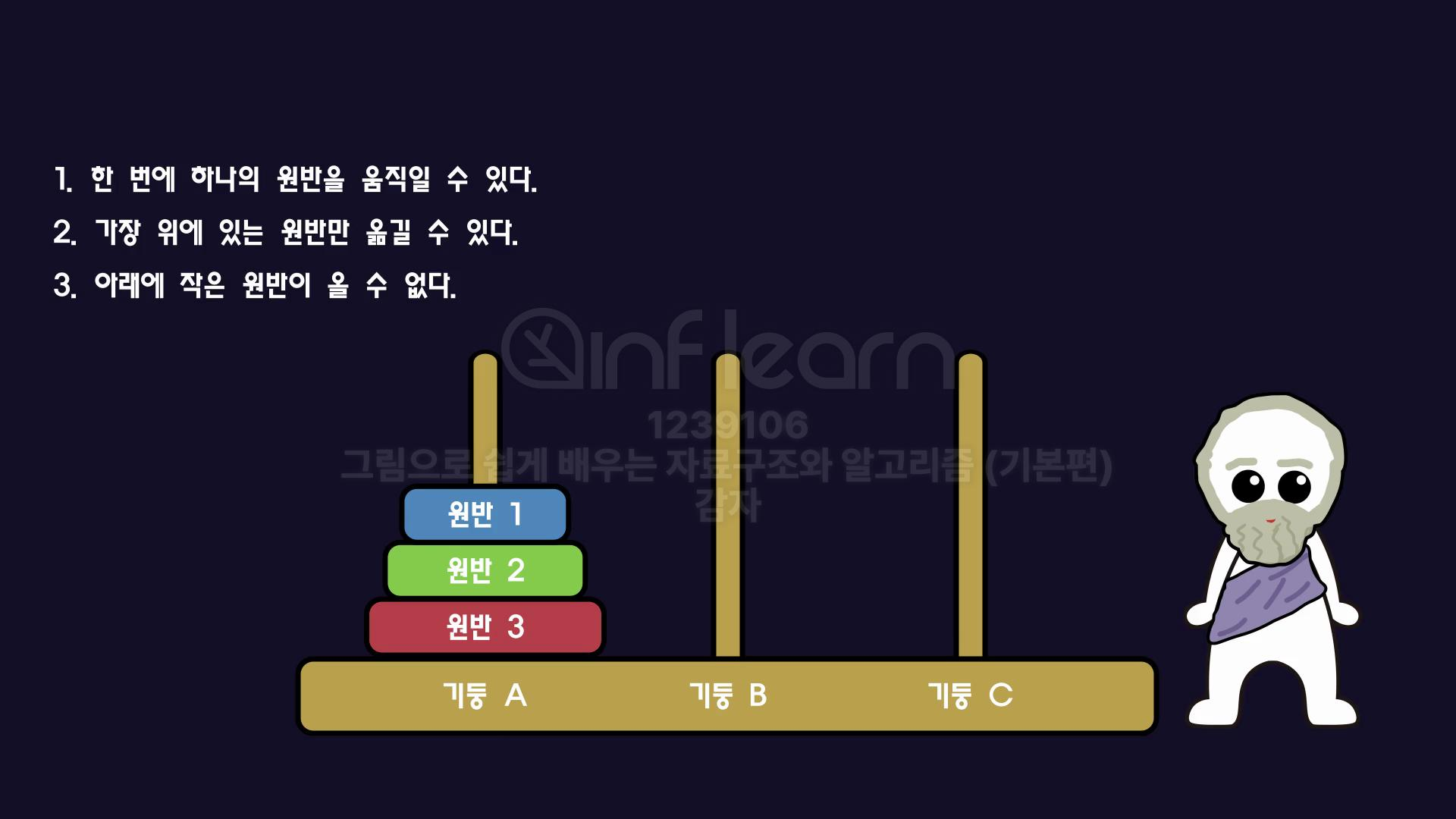
문제: 기둥 A에 꽃혀있는 3개의 크기가 다른 원반1,2,3을 기둥 B로 옮기기

기둥은 A, B, C 세 가지가 존재한다.

크기가 작은 순으로 원반1, 원반2, 원반3이 존재한다.

규칙1. 한 번에 한 개의 원반만 옮길 수 있다.

규칙2. 가장 위에 있는 원반만 옮길 수 있다.

규칙3. 작은 원반 위에 큰 원반이 올 수 없다.

위의 문제를 해결하기 위한 과정은 다음과 같다.

path1

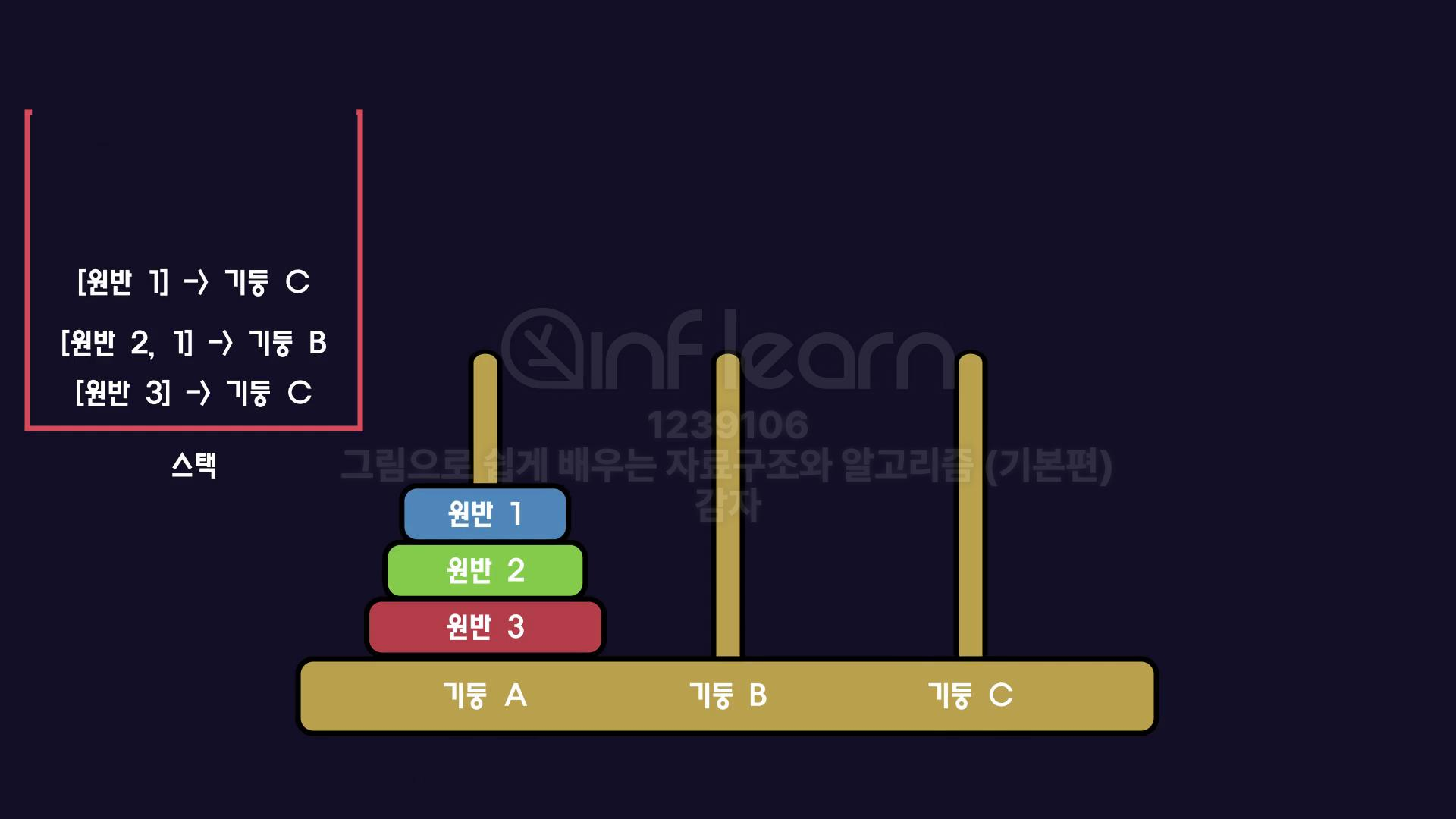
1. 기둥C로 원반3을 옮겨야 하므로 먼저 기둥B로 원반 1, 2를 옮겨야 한다.

2. 그런데 기둥B로 원반 1, 2를 옮기기 위해 먼저 기둥C로 원반 1을 옮겨야 한다.

이를 콜스택에 넣는다고 생각하면 아래와 같고, 맨 위부터 수행하면 된다.

path2

1. 기둥 B에 남아 있는 원반1,2를 기둥C로 옮겨야 한다.

2. 그런데 기둥C로 원반 1,2를 기둥C로 옮기기 위해 먼저 기둥A로 원반 1을 옮겨야 한다.

이를 콜스택에 넣는다고 생각하면 아래와 같고, 맨 위부터 수행하면 된다.

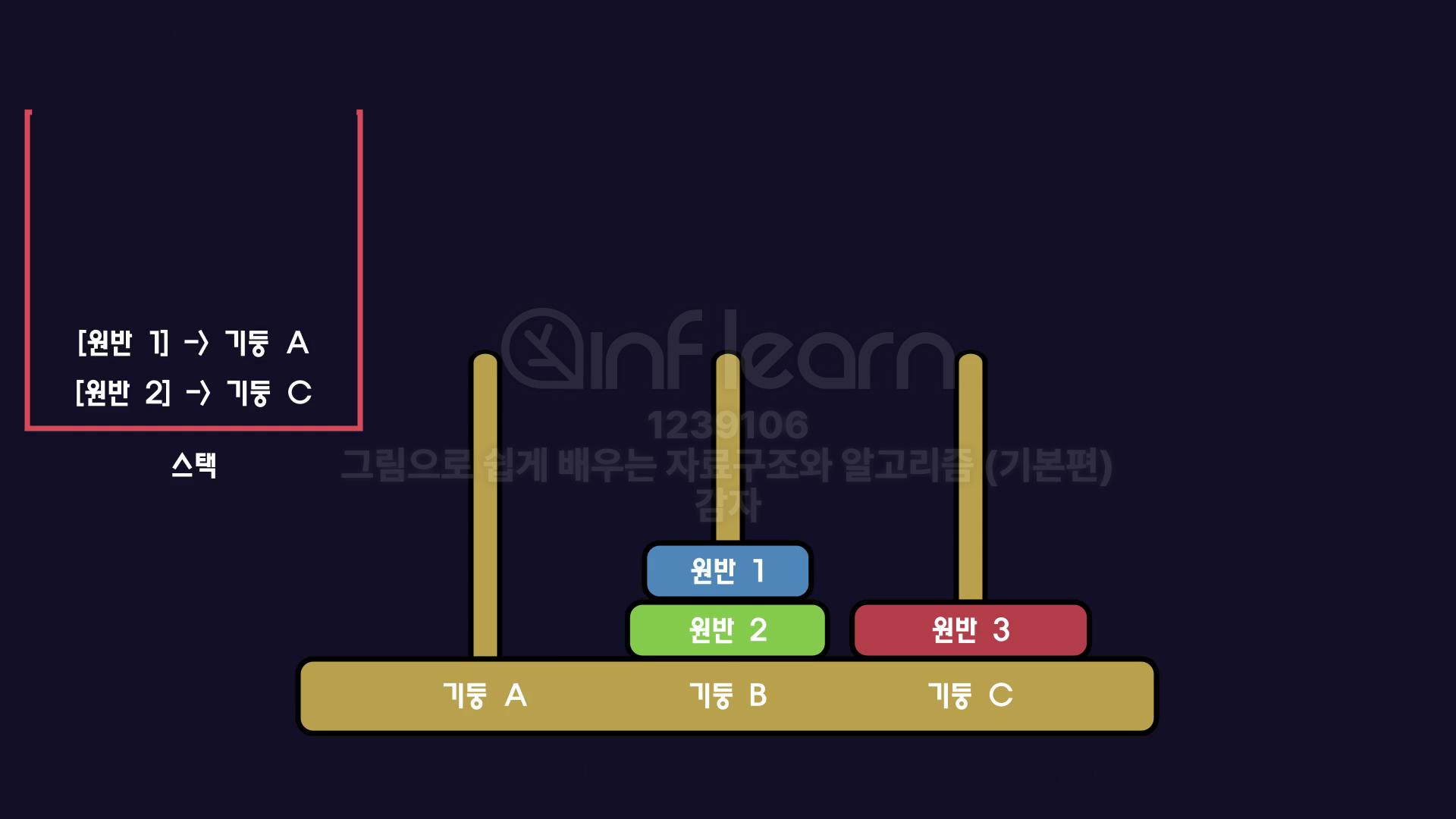
위의 흐름을 토대로 매개변수로 count, from, to, temp를 이용해 코드로 구현할 수 있다.

• 시작(From): A

• 목표(To): C

• 임시(Temp): B

버블 정렬(Bubble Sort)

왼쪽의 원소부터 인접한 원소와의 대소를 비교하여 더 큰 원소를 뒤쪽으로 보내며 자리를 바꾸는 정렬 방식

버블 정렬의 원리

다음과 같은 배열이 있다고 할 때, 버블 정렬이 진행되는 과정을 알아보자.

array = [4,2,3,1]

path 1

1-1. 4와 2를 비교해 더 큰 숫자가 앞에 있으니 둘의 자리를 바꾼다.

[2, 4, 3, 1]

1-2. 4와 3을 비교해 더 큰 숫자가 앞에 있으니 둘의 자리를 바꾼다.

[2, 3, 4, 1]

1-3. 4와 1을 비교해 더 큰 숫자가 앞에 있으니 둘의 자리를 바꾼다.

[2, 3, 1, 4]

차례대로 모든 원소를 한 번 지났으므로 path 1을 끝낸다.

가장 큰 숫자인 4가 마지막에 위치했으므로 다음 path에서는 4를 제외하고 정렬을 수행한다.

path 2

4를 제외하고 다시 맨 앞의 원소부터 비교해 나가기 시작한다.

2-1. 2와 3을 비교했지만 규칙에 맞으니 넘어간다.

[2, 3, 1, 4]

2-2. 3과 1을 비교해 더 큰 숫자가 앞에 있으니 둘의 자리를 바꾼다.

[2, 1, 3, 4]

차례대로 모든 원소를 한 번 지났으므로 path 2를 끝낸다.

다음으로 큰 수인 3이 세번 째에 잘 위치했으므로 다음 path에서는 3 또한 제외하고 정렬을 수행한다.

path 3

다시 맨 앞의 원소부터 비교해 나가기 시작한다.

2-2. [1, 2, 3, 4]

2와 1을 비교해 더 큰 숫자가 앞에 있으니 둘의 자리를 바꾼다.

모든 원소가 작은 원소부터 큰 원소 순서대로 잘 자리했으니 정렬을 마친다.

버블 정렬의 성능

버블정렬은 이해와 구현이 간단하다. 그렇다면 성능은 어떨까?

배열의 개수가 n개일 경우 정렬을 해야하는 횟수는 (n-1)+(n-2)+(n-3)+...+2+1로, 이를 식으로 표현하면 n(n-1)/2 즉, (n²-n)/2가 된다.

이를 빅 오로 표기하면 O(n²)의 성능을 갖는다고 할 수 있다. 이는 입력량에 따른 계산량이 급격하게 상승하여 좋은 성능이 아니다.

버블 정렬의 장단점

버블 정렬의 장점

• 간단한 이해와 구현이 가능

버블 정렬의 단점

• O(n²)의 낮은 성능

선택 정렬(Selection Sotr)

배열의 정렬되지 않은 영역의 첫 번째 원소를 시작으로 마지막 원소까지 비교 후 가장 작은 값을 첫 번째 원소로 가져오는 정렬 방식

선택 정렬의 원리

다음과 같은 배열이 있다고 할 때, 선택 정렬이 진행되는 과정을 알아보자.

array = [6, 3, 4, 1, 2, 5]

path 1

첫 번째 원소인 6을 시작으로 한 칸씩 옆으로 이동하며 가장 작은 원소를 찾아 첫 번째 원소와 자리를 교체한다.

[1, 3, 4, 6, 2, 5]

차례대로 모든 원소를 한 번 지났으므로 path 1을 끝낸다.

가장 작은 원소인 1이 첫번째에 위치했으므로 다음 path에서는 1을 제외한 부분에서 다시 정렬을 수행한다.

path 2

1을 제외하고 두 번째 원소부터 비교해 나아가기 시작한다.

두 번째 원소인 3을 시작으로 한 칸씩 옆으로 이동하며 가장 작은 원소를 찾아 3과 자리를 교체한다.

[1, 2, 4, 6, 3, 5]

차례대로 모든 원소를 한 번 지났으므로 path 2를 끝낸다.

두 번째로 작은 원소인 2가 두 번째에 위치했으므로 다음 path에서는 1과 2를 제외한 부분에서 다시 정렬을 수행한다.

path 3

1과 2를 제외하고 세 번째 원소부터 비교해 나아가기 시작한다.

세 번째 원소인 4를 시작으로 한 칸씩 옆으로 이동하며 가장 작은 원소를 찾아 4와 자리를 교체한다.

[1, 2, 3, 6, 4, 5]

차례대로 모든 원소를 한 번 지났으므로 path 3을 끝낸다.

세 번째로 작은 원소인 3이 세 번째에 위치했으므로 다음 path에서는 1, 2, 3을 제외한 부분에서 다시 정렬을 수행한다.

path 4

1, 2, 3을 제외하고 네 번째 원소부터 비교해 나아가기 시작한다.

네 번째 원소인 6을 시작으로 한 칸씩 옆으로 이동하며 가장 작은 원소를 찾아 6과 자리를 교체한다.

[1, 2, 3, 4, 6, 5]

차례대로 모든 원소를 한 번 지났으므로 path 4를 끝낸다.

네 번째로 작은 원소인 4가 네 번째에 위치했으므로 다음 path에서는 1, 2, 3, 4를 제외한 부분에서 다시 정렬을 수행한다.

path 5

1, 2, 3, 4를 제외하고 다섯 번째 원소부터 비교해 나아가기 시작한다.

다섯 번째 원소인 6을 시작으로 한 칸씩 옆으로 이동하며 가장 작은 원소를 찾아 6과 자리를 교체한다.

[1, 2, 3, 4, 5, 6]

차례대로 모든 원소를 한 번 지났으므로 path 5를 끝낸다.

다섯 번째로 작은 원소인 5가 다섯 번째에 위치했으며 하나 남은 원소 6은 자동으로 정렬되어 모든 원소가 작은 원소부터 큰 원소 순서대로 잘 자리했다.

정렬을 마친다.

선택 정렬의 성능

선택 정렬은 이해와 구현이 간단하다. 그렇다면 성능은 어떨까?

배열의 개수가 n개일 경우 정렬을 해야하는 횟수는 (n-1)+(n-2)+(n-3)+...+2+1로, 이를 식으로 표현하면 n(n-1)/2 즉, (n²-n)/2가 된다.

이를 빅 오로 표기하면 O(n²)의 성능을 갖는다고 할 수 있다. 버블 정렬과 같은 성능이라고 할 수 있다.

선택 정렬의 장단점

선택 정렬의 장점

• 간단한 이해와 구현이 가능

선택 정렬의 단점

• O(n²)의 낮은 성능

운영체제(Operating System)

CPU 스케줄링

스케줄링의 성능 평가

CPU 스케줄링의 성능을 평가하는 기준은 다음과 같다.

평균 대기 시간

프로세스 여러 개 실행시 모든 프로세스가 실행되기까지의 대기 시간의 평균

CPU 스케줄링의 종류

FIFO(First In First Out)

스케줄링 큐에 들어온 순서대로 CPU를 할당 받는 방식으로, 먼저 들어온 프로세스의 실행이 완전히 끝나야만 다음 프로세스 실행이 가능하다. ex) 마트 계산대

장점

• 단순하며 직관적

단점

• 한 프로세스가 완전히 끝나야만 다음 프로세스 진행이 가능하다는 점에서 실행 시간이 짧고 늦게 도착한 프로세스가 실행 시간이 길고 빨리 도착한 프로세스의 작업을 기다려야 한다는 것

• I/O 작업이 있을 시 CPU는 작업이 끝날 때 까지 쉬기 때문에 낮은 효율성

평균 대기 시간

• Burst Time이 짧은 프로세스 먼저 실행시 평균 대기 시간이 짧다.

• Burst Time이 긴 프로세스 먼저 실행시 평균 대기 시간이 길다.

프로세스의 Burst Time에 따라 평균 대기 시간의 차이가 크기 때문에 잘 쓰이지 않고, 일괄처리 시스템에 사용된다.

 SJF(Shortest Job First)

FIFO 스케줄링에서 발견한 특징에 의해 고안된 스케줄링 방법으로, Burst Time이 짧은 프로세스를 먼저 실행하는 방식이다.

이는 이론적으로는 FIFO보다 성능이 더 좋지만 문제점이 있다.

• 어떤 프로세스가 얼마나 실행될지 예측 불가

• Burst Time이 긴 프로세스는 Burst Time이 짧은 프로세스 작업이 계속 들어올 시 순서가 계속 밀려나 아주 오랜 시간 동안 실행되지 못할 수 있다.

RR(Round Robin)

FIFO 스케줄링의 단점을 해결하기 위해 고안된 스케줄링 방법으로, 각 프로세스에게 일정 시간만큼 할당하여, 실행 중이던 프로세스의 할당 시간이 끝나면 CPU 할당을 끝내고 큐의 가장 뒤로 위치 시킨 뒤 다음의 프로세스를 실행하는 방식이다.

타임 슬라이스(타임 퀀텀)

프로세스에게 할당하는 일정 시간

평균 대기 시간

• 타임 슬라이스 값에 따라 크게 달라진다.

• 타임 슬라이스 값이 아주 클 경우, FIFO 알고리즘과 같은 평균 대기 시간을 가진다.

• 타임 슬라이스 값이 아주 작을 경우, 잦은 컨텍스트 스위칭 발생으로 오버헤드가 커진다.

그러므로 사용자가 프로세스가 끊기지 않고 동시에 실행되는 것처럼 느끼면서 가장 큰 타임 슬라이스 값을 찾아야 한다.

 MLFQ(Multi Level Feedback Queue)

RR 스케줄링을 기반으로 만들어졌으며 운영체제는 CPU Bound Process와 I/O Bound Process를 구분하며 CPU Bound Process는 타임 슬라이스를 크게, I/O Bound Process는 타임 슬라이스를 작게 주는 방식으로, 오늘날 운영체제에서 가장 일반적으로 쓰이는 스케줄링 기법이다.

타임 슬라이스 선택 방식

우선순위가 낮을수록 타임 슬라이스 크기가 커지고, 우선순위가 높을수록 타임 슬라이스 크기가 작은 큐 여러 개가 존재.

모든 프로세스는 높은 우선순위의 큐에서 시작해 점점 큰 타임 슬라이스를 가진 낮은 우선순위의 큐까지 한칸씩 내려가며 만족하는 타임슬라이스를 가지는 우선순위 큐에 위치한다.

CPU 사용률이 높은 프로세스의 경우 타임 슬라이스가 크므로 낮은 우선순위 큐에 많이 위치하게 되고, I/O 사용률이 높은 프로세스의 경우 타임 슬라이스가 작으므로 높은 우선순위 큐에 많이 위치한다.

프로세스 동기화

독립 프로세스와 협력 프로세스

운영체제 내에서 프로세스들이 상호작용하는 방식에 따라 독립 프로세스(Independent Processes)와 협력 프로세스(Cooperating Processes)로 구분한다.

독립 프로세스(Independent Processes)

독립 프로세스는 다른 프로세스의 실행에 영향을 받지 않으며, 다른 프로세스에 영향을 주지도 않는 프로세스이다.

독립 프로세스의 특징

• 자원의 독립성: 자신의 메모리 공간과 시스템 자원 독립적 사용

• 실행의 독립성: 프로세스의 실행이 다른 프로세스의 상태나 실행에 비의존

• 통신의 부재: 프로세스 사이에 명시적인 데이터 공유 또는 통신 부재

협력 프로세스(Cooperating Processes)

협력 프로세스는 다른 프로세스와 데이터를 공유하거나, 어떤 방식으로든 서로 영향을 주고받는 프로세스

협력 프로세스의 특징

• 데이터 공유: 프로세스간 데이터 또는 자원의 공유

• 동기화: 프로세스 작업의 진행 속도에 따라 서로 동기화 가능

• 통신: 프로세스 간 통신을 통해 서로 정보 교환

그렇다면 협력 프로세스는 데이터를 공유하고, 작업을 조율하기 위해 어떻게 통신할까?

프로세스의 통신 종류

• 스레드 간 통신(Thread Communication)

한 프로세스 내에서의 통신

프로세스 내의 쓰레드는 코드, 데이터, 힙영역 공유하고 스택은 자기 것을 소유하는데 이 중 데이터 영역에 있는 전역변수나 힙을 통해 통신

• 프로세스 간 통신(Inter-Process Communication, IPC)

한 컴퓨터 내에서의 프로세스 간 통신

파일을 이용한 읽고 쓰기

운영체제가 생성한 파이프를 이용해 데이터를 읽고 쓰기

다른 컴퓨터의 다른 프로세스 간 통신

운영체제가 제공하는 소켓을 통한 통신

다른 컴퓨터에 있는 함수를 호출하는 RPC(원격 프로시저 호출)를 이용해 통신

공유자원과 임계구역

공유자원이란?

프로세스 간 통신(IPC)을 할 때 공동으로 이용하는 변수나 파일

이 공유자원에 여러 프로세스가 동시에 접근할 때 발생할 수 있는 상황을 경쟁조건(Racing Condition)이라고 하며 그 상황에서 발생할 수 있는 문제는 다음과 같다.

• 여러 프로세스가 공유하기 때문에 각 프로세스의 접근 순서에 따라 결과가 달라질 수 있다.

• 컨텍스트 스위칭으로 시분할 처리를 하기 때문에 어떤 프로세스가 언제 처리될지 모른다.

• 연산 결과를 예측하기 힘들다.

위와 같은 문제들로 인해 임계구역 관리가 필요하다.

임계구역(Critical Section)이란?

여러 프로세스가 동시에 사용하면 안되는 영역으로, 임계구역 내의 코드를 실행하는 동안 해당 자원에 대한 독점적인 접근이 보장되어야 한다. 이는 동시 실행되는 프로세스나 스레드 사이에서 데이터의 일관성과 무결성을 유지한다.

 

임계구역 문제 해결을 위한 조건

상호 배제(Mutual Exclusion) 메커니즘

상호 배제 매커니즘의 요구사항 3가지

• 임계영역엔 동시에 하나의 프로세스만 접근

• 동시에 여러 요청이 있을 경우에도 하나의 프로세스 접근만 허용

• 임계구역에 들어간 프로세스는 빠르게 다시 나옴

임계구역 문제 해결 기법

1. 세마포어(Semaphore)

공유자원을 필요로 하는 프로세스들은 대기 큐에 순서대로 대기 하고 먼저 온 프로세스에게 세마포어(정수형 변수=공유 변수의 개수, 예를 들어 공유 변수가 한 개일 때 s = 1)를 부여한다. 해당 프로세스의 실행이 끝나고 부여된 세마포어가 반납될 때 까지 다음의 프로세스는 이 세마포어를 받기 위해 기다려야 하는 방식

예를 들어 코드로 살펴보자면 아래와 같다.

먼저 온 프로세스는 wait() 함수로 세마포어를 부여 받고, 코드를 실행해 나간다. 이후에 온 프로세스는 세마포어를 부여 받기 위해 기다렸다가 이전의 프로세스가 코드 실행을 마치고 signal() 함수로 세마포어를 반납하면 그 때 세마포어를 부여 받을 수 있다.

wait(변수);
실행 코드;
signal(변수);

세마포어의 단점

wait() 함수와 signal() 함수의 위치를 실수로 바꿔 잘못 사용할 가능성 존재

2. 모니터(Monitor)

세마포어의 단점을 해결한 상호 배제 메커니즘으로, 운영체제가 아닌 프로그래밍 언어 차원에서 지원하는 방법

wait() 함수와 signal() 함수로 해당 코드를 감쌀 필요 없이 프로그래밍 언어가 지원하는 언어로 간편하고 안전하게 상호 배제 메커니즘을 실현할 수 있다.

예를 들어 JAVA에서는 임계구역을 표시하기 위해 동기화된 메서드 'synchronized method'를 사용한다. synchronized 구문이 실행되는 동안 여러 프로세스에서 모니터를 점유하려고 시도해도 할 수 없으며 해당 구문이 끝날 때까지 대기해야 한다.

교착상태(Deadlock)

여러 프로세스가 서로 다른 프로세스의 작업이 끝나기를 기다리다 어떤 프로세스도 작업을 진행하지 못하는 상태로, 시스템의 자원을 비효율적으로 사용하게 만들며 최악의 경우 시스템의 정지를 초래할 수 있다.

발생 이유

공유 자원을 통해 여러 개의 프로세스가 자원을 공유하기 때문

필요 조건

교착상태가 발생하려면 다음의 네 가지 조건을 모두 충족해야 한다.

• 상호 배제: 어떤 프로세스가 리소스를 점유 했다면 다른 프로세스에게 해당 리소스는 공유 되면 안된다.

• 비선점: 어떤 프로세스가 리소스를 점유 했다면 다른 프로세스는 해당 리소스를 빼앗을 수 없다.

• 점유와 대기: 어떤 프로세스가 리소스를 가지고 있는 상태에서 다른 리소스를 원하는 상태

• 원형 대기: 점유와 대기를 이루는 프로세스들이 원형을 이루는 형태

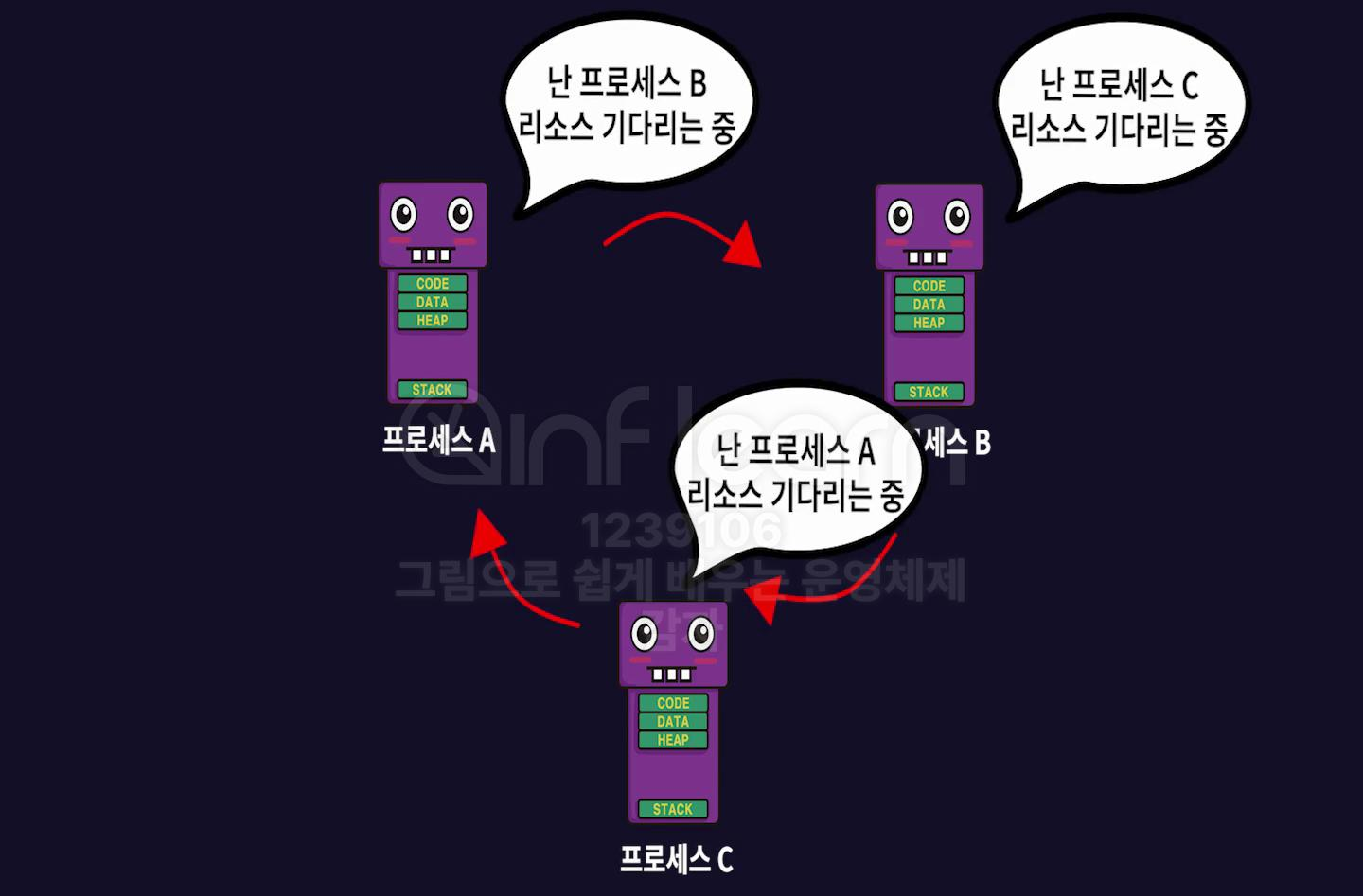
교착 상태 해결

교착 상태 회피(Deadlock Avoidance)

프로세스에 자원을 할당할 때 어느 정도 할당해야 교착 상태가 발생하는지 파악하여 교착 상태가 발생하지 않는 수준의 자원을 할당하는 방법

전체 자원의 수와 할당된 자원의 수를 기준으로 안정 상태와 불안정 상태로 나눈다.

안전 상태는 시스템이 프로세스의 모든 추가 요구를 충족시킬 수 있는 충분한 자원을 가지고 있어서, 모든 프로세스가 교착 상태 없이 실행을 완료할 수 있는 상태이며 불안전 상태는 교착 상태에 빠질 확률이 높아진 상태이다.

운영체제는 최대한 안정 상태를 유지하기 위해 자원을 할당

은행원 알고리즘(Banker's Algorithm)

다익스트라(Edsger W. Dijkstra)에 의해 고안된 교착 상태 회피 알고리즘 중 하나

운영체제는 프로세스에 자원을 할당하기 전에 자신이 가지는 총 자원의 수(시스템 총 자원의 수)를 미리 알고 있어야 하며 각 프로세스는 자신이 필요한 최대 자원의 수(최대 요구 자원)를 운영체제에 미리 알린다.

위의 안정 상태에서 P1이 자원 요청을 할 경우 예상 자원이 사용 가능한 자원인 2보다 크기 때문에 자원을 할당하지 않는다.

P2가 자원 요청을 하면 예상 자원이 사용 가능한 자원으로 할당 가능하기 때문에 P2에게 자원 2개를 할당 하고, P2는 2개의 자원을 더 받아 작업을 마치고 총 6개의 자원을 반납한다.

사용 가능한 자원이 6개가 됐으므로 P1에 자원을 할당 할 수 있게 되어 자원 4개를 할당한다.

반면 위와 같은 불안정 상태에서는 사용 가능한 자원이 1개뿐인데 반해 모든 프로세스의 요청 예상 자원이 2개로, 어떤 프로세스에게도 자원을 할당해 주지 못한다.

하지만 프로세스가 최대 자원을 요청하지 않는다면 교착 상태에 빠지지 않을 수도 있다. 그래도 불안정 상태에 빠지지 않도록 유지하는 것이 좋다.

은행원 알고리즘의 단점

• 높은 비용

• 비효율적

위의 단점으로 인해 교착 상태의 발생은 허용하고, 교착 상태가 발생했을 때 해결하는 방식을 연구했다.

교착상태 검출 방식

1. 가벼운 교착 상태 검출

타이머를 이용해 프로세스가 일정 시간 동안 작업을 진행하지 않는 상태 검출

교착 상태 해결

일정 시점마다 체크포인트를 만들어 작업 저장해놓은 뒤 타임 아웃으로 교착상태가 발생할 시 마지막으로 저장했던 체크포인트로 롤백

2. 무거운 교착 상태 검출

자원 할당 그래프(Resource Allocation Graph)를 이용해 운영체제는 프로세스가 어떤 자원을 사용하는지 지켜보다가 교착 상태가 발생 시 검출

이 그래프에서 교착 상태는 순환 대기(circular wait) 조건을 만족하는 사이클로 나타난다.

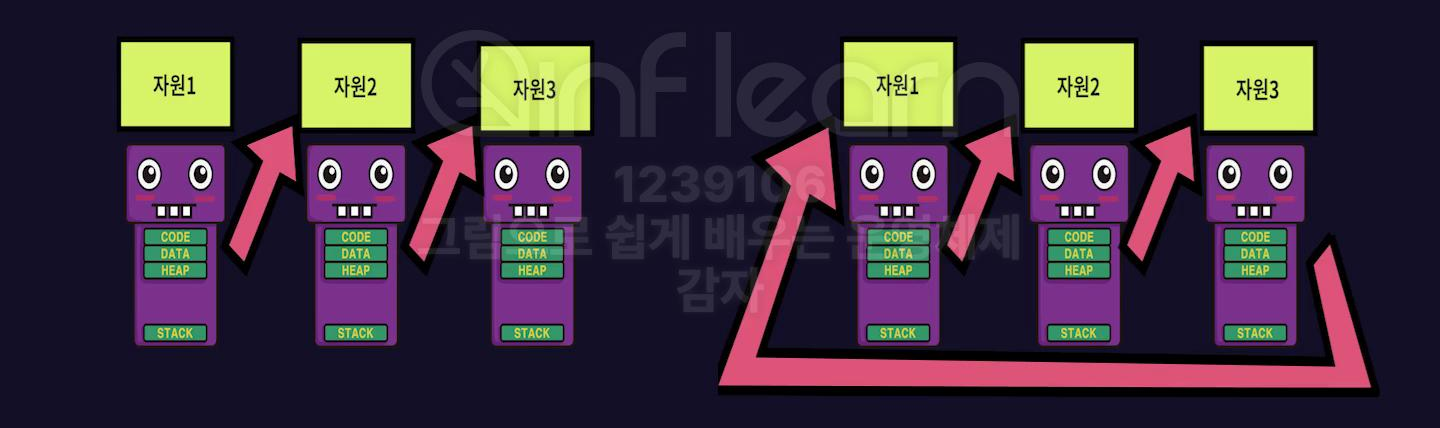
교착 상태 해결

교착 상태를 일으킨 프로세스 강제 종료 시킨 뒤 다시 실행시킬 때 체크포인트로 롤백 시킨다.

단점

운영체제가 지속적으로 자원 할당 그래프를 유지하고 검사해야해 오버헤드 발생

메모리의 종류

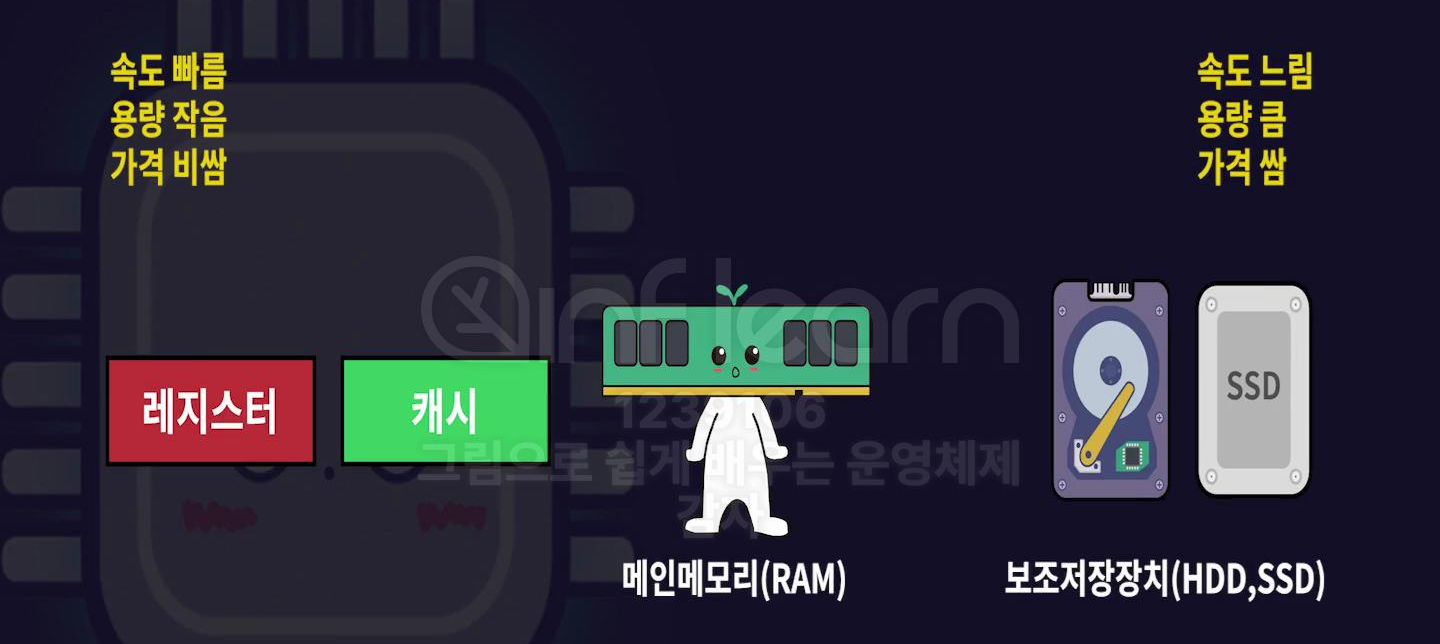
레지스터

가장 빠른 기억 장소로, CPU 내 위치. 컴퓨터가 꺼지면 데이터가 사라져 휘발성 메모리라고 부른다. 32bit, 64bit 등으로 크기를 구분해 32bit 레지스터를 가지는 CPU를 32bit CPU, 64bit 레지스터를 가지고 있으면 64bit CPU라고 한다.

CPU는 계산을 할 때 메인 메모리에 있는 값을 레지스터로 가져와 계산, 계산 결과는 다시 메인 메모리에 저장한다.

어셈블리 코드를 보면 기계어와 1:1 매칭이 되어 실제로 레지스터를 사용하는 것을 볼 수 있다.

캐시

레지스터와 메인 메모리 사이에 존재하는 휘발성 메모리.

레지스터는 속도가 매우 빠른 반면 메인 메모리는 속도가 느린 편이다. 메인 메모리에 있는 데이터를 레지스터로 옮기려면 오랜 시간이 걸리기 때문에 필요 할 것 같은 데이터를 미리 저장해 두는 역할을 한다. 성능의 이유로 여러개(L1, L2, L3..)를 둔다.

메인 메모리

실제 운영체제와 다른 프로세스들이 올라가는 공간으로, 전원이 공급되지 않으면 데이터가 지워지는 휘발성 메모리.

하드디스크나 SSD보다 속도는 빠르지만 가격이 비싸 데이터 저장보단 실행 중인 프로그램만 올리는 용도

보조 저장장치(SSD, 하드디스크)

가격이 저렴하고 전원이 공급되지 않아도 데이터를 저장하는 비휘발성 메모리

메모리의 구조

오늘날의 컴퓨터는 CPU와 메인 메모리가 함께 사용되어 모든 프로그램을 메모리 위로 올려 실행하는 폰 노이만 구조로, 하나의 프로그램만 메모리에 올라가던 예전에 비해 관리하기가 복잡해졌다.

메모리는 1Byte(8bit)마다 주소를 가진다.

32bit CPU는 레지스터 크기, ALU(산술논리연산장치), 버스의 크기가 32bit이며 CPU가 다룰 수 있는 메모리도 2³²으로 4GB이다.

64bit CPU도 레지스터 크기, ALU(산술논리연산장치), 버스의 크기가 64bit이며 CPU가 다룰 수 있는 메모리도 2⁶⁴으로 거의 무한대에 가깝다.

메모리를 컴퓨터에 연결하면 0번지부터 주소가 있다. 이를 물리 주소 공간이라 한다.

사용자 관점에서의 공간은 논리 주소 공간이며, 이를 통해 물리 주소 공간에 접근한다.

메모리는 운영체제 영역을 따로 가지고 있어 이 영역이 침범 되면 위험할 수 있다.

경계 레지스터

CPU 내에 존재하는 레지스터로, 하드웨어적으로 운영체제 공간과 사용자 공간을 나눈다. 메모리 관리자가 사용자 프로세스가 경계 레지스터 값을 벗어났는지 검사하고 만약 벗어났다면 그 프로그램을 강제 종료한다.

절대주소와 상대주소

사용자가 상대주소(논리주소)로 접근 시 메모리 관리자는 재배치 레지스터에 있는 프로그램의 시작 주소를 가지고 있어, 이 시작 주소에 상대주소를 더한 절대 주소(물리 주소)를 찾는다.

메모리 관리자를 통해 모든 사용자 프로세스는 0x0번지부터 시작한다는 가정으로 편리하게 프로그램을 만들 수 있다.

메모리 할당 방식

유니 프로그래밍 환경

메모리 오버레이

메모리보다 큰 프로그램을 실행하면 당장 필요한 부분만 먼저 메모리에 올리고 나머지 부분은 하드디스크의 스왑 영역에 저장하는 기법

하지만 이는 스왑 영역에 있는 데이터 일부를 메모리로 옮기고, 메모리에 있는 데이터를 스왑 영역으로 옮기는 과정이 필요하기 때문에 동작이 느리다.

멀티 프로그래밍 환경

1. 가변 분할 할당(Dynamic-Partition Allocation, 세그멘테이션)

프로세스의 크기에 따라 메모리를 할당하는 방식

장점

• 프로세스 크기에 맞게 메모리가 할당되어 내부 단편화가 없다

내부 단편화란?

프로세스의 크기가 할당된 메모리 크기보다 작을 경우 발생되는 메모리 낭비 공간

단점

• 메모리의 할당과 회수 과정에서 작은 메모리 공간이 여러 곳에 분산될 수 있다. 이 공간을 합친 총 메모리 공간이 충분함에도 연속된 공간이 아니기 때문에 크기가 큰 프로세스가 들어갈 수 없어 낭비되는 외부 단편화 발생

• 가변 분할 방식에서 외부 단편화가 생기는 경우 그 공간들을 합쳐주는 조각 모음을 실행하면 문제가 해결되지만 실행중인 다른 프로세스들을 중지하고 위치를 옮기는 과정이 필요해 오버헤드 발생

2. 고정분할 할당 (Fixed-Partition Allocation, 비연속 메모리 할당, 페이징)

프로세스 크기와 상관없이 고정된 크기의 메모리를 할당하는 방식

장점

• 구현이 간단하고 오버헤드가 적다

단점

• 프로세스의 크기가 할당된 고정 메모리 크기보다 작을 경우 내부 단편화 발생

• 분할되는 크기를 조절해 내부 단편화를 최소화 해줘야 한다.

3. 버디 시스템

2의 승수로 메모리를 분할해 메모리 할당하는 방식으로, 가변 분할 할당 방식과 고정분할 할당 방식을 혼합해 단점을 줄임

장점

• 프로세스 크기에 따라 할당되는 메모리 크기가 달라지며 외부 단편화를 방지하기 위해 메모리 공간을 확보하는 것이 간단하다.

• 내부 단편화가 발생하긴 하지만 공간 낭비가 적다.

회고

 지난 주에 이어 알고리즘 같은 경우에는 강의를 보며 따라하기 전에 내가 미리 구현 해보는 시간을 가짐으로써 지난 주에 가졌던 아쉬움을 타파해보려고 노력한 점을 칭찬해주고 싶다. 보고 따라 치는 것만 하는 것 보다 먼저 구현해 봄으로써 내가 어떻게 사고하고 있고, 잘 안 됐던 부분에서는 어떤 지점에서 사고가 부족했는지 확실히 알 수 있었다.

운영체제의 경우 강의를 토대로 다른 자료들도 함께 봄으로써 조금 더 폭넓게 이해하려고 노력했다. 그러다보니 생각보다 시간이 많이 소요되기도 한다. 정해진 시간 안에 조금 더 효율적으로 공부할 수 있도록 루틴을 짤 필요가 있을 것 같다.