

인프런 커뮤니티 질문&답변
PCA 개념에 대해 질문이 있습니다.
해결된 질문
작성
·
581
0
PCA 관련하여 학습 중 궁금한 점이 생겨 질문드리게 되었습니다.
1. 책 380쪽에 보면 '...생략... 세 번째 축은 다시 두 번째 축과 직각이 되는 벡터를 설정하는 방식으로 축을 생성합니다.' 라고되어 있는데 아래의 그림처럼 축을 생성하는건가요?
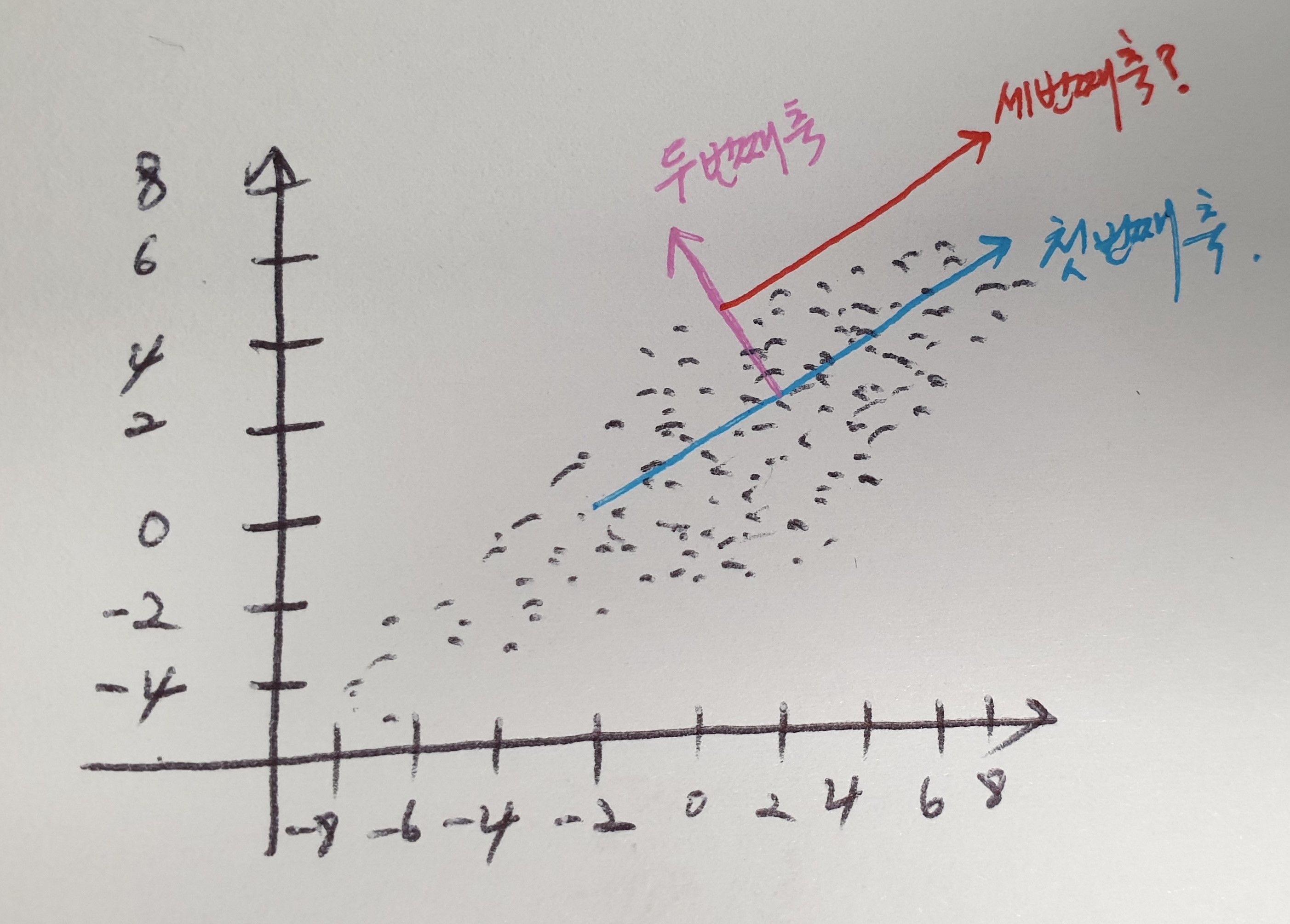
이렇게 축을 생성해서 379 페이지에 있는 그림처럼 축에 투영(투영한다는 말이 맞는지 모르겠네요)하여 차원을 2차원에서 1차원으로 축소한다는 것으로 이해하고 있는데 맞는건가요?
그리고 축을 왜 세 개나 만들어야 할까요?
2. 381 페이지에 중간쯤 '...생략... 대칭행렬은 항상 고유벡터를 직교행렬로, 교유값을 정방 행렬로 대각화할 수 있다는 것 입니다.' 라는 말이 있는데 여기서 '직교행렬'이 뜻하는 게 뭔지 잘 모르겠습니다.
구글링을 하며 학습할려고 했는데 수학을 몰라 이해가 되지 않네요.
3. '고유벡터'는 그냥 임의의 값인건가요?
답변 주시면 감사하겠습니다.
답변 3
1
네, 맞습니다. 그림처럼 축이 만들어집니다. 덧붙이자면, 축이라는 표현은 설명의 이해를 돕기 위해서이며, 정확히는 축소하려는 차원만큼 고유 벡터들이 만들어지고 이를 이용해 선형 변환을 하는 것입니다.
교수님이라면 표현은 너무 과분합니다(기분은 좋습니다 ^^). 강사로 충분할 거 같습니다. 감사합니다.
1
안녕하십니까,
그림을 아주 잘 그리셨습니다.
1. PCA 축을 만드는 것은 PCA로 차원 축소될 최종 차원을 결정하는 방식입니다. 가령 3차원 원본 데이터를 2차원으로 차원 축소하려면 PCA축을 2개 만들게 됩니다. 2차원 원본 데이터를 1차원으로 축소하려면 PCA축은 1개만 있으면 됩니다. 10차원 원본 데이터를 3차원으로 축소하려면 PCA축은 3개만 있으면 됩니다.
이때 축을 생성하는 순서는 원본 데이터에 분산이 큰 방향성을 가진 벡터를 기반으로 축을 생성했으면, 두번째 축은 거기에 직각인 축, 세번째 축은 다시 두번째 축의 직각인 축으로 생성하게 됩니다. 그리고 이렇게 만들어 진 축에 원본 데이터를 투영하여 차원 축소를 하게 됩니다.
2. PCA의 수학적 기반을 이해하는 것은 시간이 많이 소모되어서 강의와 책에서 이렇게 요약 드렸습니다.
'입력 데이터의 공분산 행렬이 고유 벡터와 고유 값으로 분해 될 수 있으며, 이렇게 분해된 고유 벡터를 이용해 원본 입력데이터를 선형 변환 하는 방식'
분해된 고유 벡터가 바로 PCA 축입니다. 고유값이 가장 큰 고유 벡터가 첫번째 PCA 축이며, 두번째로 고유값이 큰 고유 벡터가 두번째 PCA 축입니다. 두번째 고유 벡터는 첫번째 고유 벡터에 직각 방향성을 가지게 됩니다.
직교 행렬은 여기서 설명 드리는것 보다는 아래 URL이 더 자세한 설명이 될 것 같아서 첨부 드립니다.
앞에서도 잠깐 언급 드린바와 같이 PCA의 수학적 기반을 이해하려면 먼저 선형대수 기반 지식이 뒷받침 되어야 하는데, 이는 PCA 이해를 위해서 너무 많은 시간을 소모하게 되기 때문에
'입력 데이터의 공분산 행렬이 고유 벡터와 고유 값으로 분해 될 수 있다' 정도만 강하게 기억해 주시면 좋을 것 같습니다.
감사합니다.
0
답변 감사합니다!
추가적인 질문이 있어서 답글 남겨 봅니다.
1. 교수님이 말씀하신 것 처럼 축소할려는 차원에 맞춰서 축이 생성된다는 거죠? 제가 그린 그림처럼 축이 만들어지는 게 맞다는 말씀이시죠?
답변 주시면 감사하겠습니다.
