

인프런 커뮤니티 질문&답변
4.5 3p 질문
해결된 질문
작성
·
285
0

안녕하세요,
여기서 eigenvalue를 구한 다음에 A*(1, -i) 형태로 이어지는 부분이 이해되지 않습니다. 어떤 방식으로 eigenvector를 구한 것인지 설명 부탁드립니다!
답변 2
0
조범희 (타블렛깎는노인)
지식공유자
Ax = ix (혹은 -ix)
의 식을 토대로 (A - i I) x = 0 의 해를 구한 것 입니다.
단지 우리가 다뤘던, real 말고 허수를 적용했다라는 차이만 있을 뿐입니다.

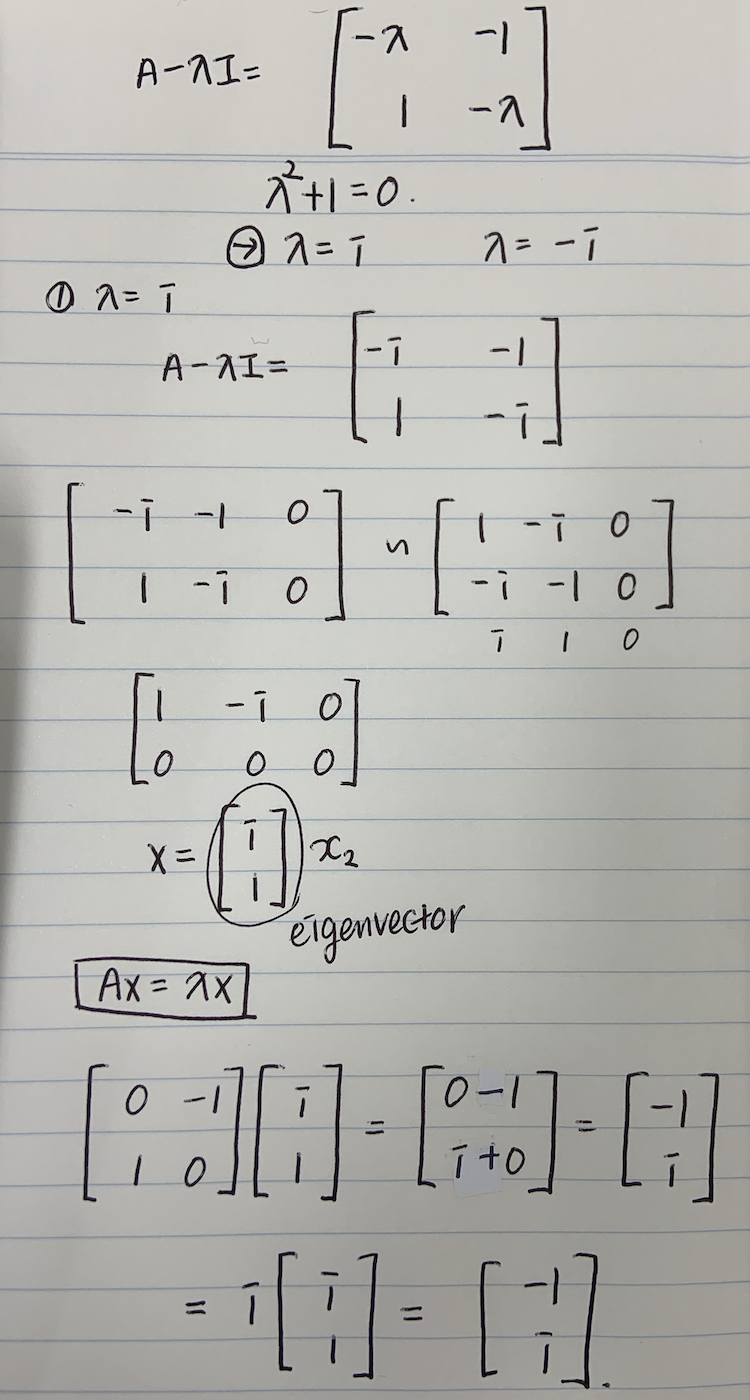
1) 맞습니다.
2) eigenvector를 v라고 해봅시다. 그럼 임의의 스칼라(a)를 곱함 a*v도 역시 eigenvector에 해당합니다. 물론 여기선 스칼라가 이제 허수여도 됩니다. 즉, 구하신답변에서 -i (답변에서 a에 해당하는 스칼라값)를 곱하게되면 (1, -i)가 나오는걸 알수있습니다. 아무튼 올바르게 구하셨습니다. 제가 구한 형태로 꼭 바꿔야하는 그런 법은 없습니다.