인프런 커뮤니티 질문&답변
작성한 질문수
4.1 EigenVector Theorem 2질문입니다.
작성
·
326
·
수정됨
0
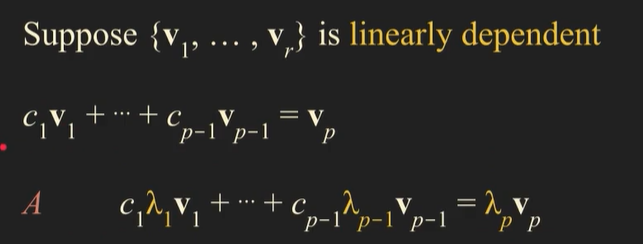
이 식에서
왜 n*n Matrix A를 Multiplication하면 저런 식이 나온다는건지 이해가 안됩니다.
그러니까, matrix A의 정의가 무엇인지 모르겠습니다.
그냥 n * n Matrix A라고만 나오는데 어떻게 A와 multiplication을 하면 저런식이 나오는건가요?
Matrix A가 어떻게 원래 식에 순차적으로 EigenValue를 곱하는 역할을 하는지 구조적으로 이해를 못하겠습니다..
추가 질문입니다. Matrix A가 Triangular Matrix일때, diagonal term은 모두 A의 EigenValue라고 했습니다.
그런데 애초에 Matrix A가 Triangular Matrix로 주어질때만 이 공식이성립하는것인가요?
Row operation을 통해서 기존의 Matrix A의 형태를 TriangularMatrix로 만들고 나서 row operation으로 만들어진 TriangularMatrix의 diagonal term을 EigenValue로 고르니까 틀린 값이 얻어졌습니다.
A에서 row operation해서 만들어진 Matrix는 결국 같은 Matrix 아닌가요? 어째서 row operation을 통해서 얻어진 Matrix의 EigenValue가 기존 Matrix A의 EigenValue와 달라지는지 궁금합니다.
답변 2
1
첫번째 질문에 대한 답은
eigenvalue 정의해 의해서 v를 eigenvector라고하고 lamda를 eigenvalue라고 하면 Av = lambda*v 이기 때문입니다.
두번째 질문에 대한 답은
row operation에 의해 만들어진 matrix는 같은 matrix가 아닙니다.
전반적인 복습이 다시 필요할것같습니다.
0
아하 드디어 이해했네요... Av = lambda*v로 생각하면 되는군요 .. 감사합니다
그러면 혹시 두번째 질문에서
row operation으로 만들어지는 linear system은 같은 solution을 가질뿐이지 서로 같은 성질을 가지는건 아니군요?
저도 질문하면서 column space부분에서 얘기해주신 성질이 약간 걸리긴 했었는데 답변받으니 이해가 잘 된 것 같습니다 감사합니다!
비슷한 성질을 지닐순있어도 어찌됐건 다른 matrix라는점은 변함없습니다!