인프런 커뮤니티 질문&답변

안녕하세요 진살라진님 ㅎㅎ

Q1. 176의 의미가 정확히 무엇인가요? 176가지인가요?

>> 네 이 문제는

"총 몇 개의 경우의 수가 있는지 말하라."

입니다. 그래서 176개의 경우의 수가 있다는 것을 의미합니다.

Q2. return check(sum); 의 결과는 1 또는 0인데 cout << go(0,0) << "\n"이 176이 되는 작동 원리가 뭔가요? return된 값을 들고 있는 go()가 다른 go()에 반환할 때 누적되어서 go(0,0)까지 쌓이는건가요?

네 맞습니다. 코드를 보면 go는 go로부터 파생된 값들의 합으로 이루어져 있습니다.

int go(int idx, int sum){
	if(idx == n){
		//cout << "SUM " << sum << "\n";
		return check(sum); 
	}
	return go(idx + 1, sum + v[idx]) + go(idx + 1, sum);
}

Q3. go()함수에서 return go(idx+1, sum + v[idx]) + go(idx+1, sum)과 같이 idx위치의 숫자를 더한 것과 더하지 않은 go()함수끼리 더하는 논리적 근거는 무엇인가요? 즉, 왜 더해야 했는지. 왜 return이라는 키워드를 사용해야 했는지 궁금합니다.

음.. 이 문제는 경우의 수를 구하는 문제입니다.

예를 들어 이런 그래프를 들어볼게요.

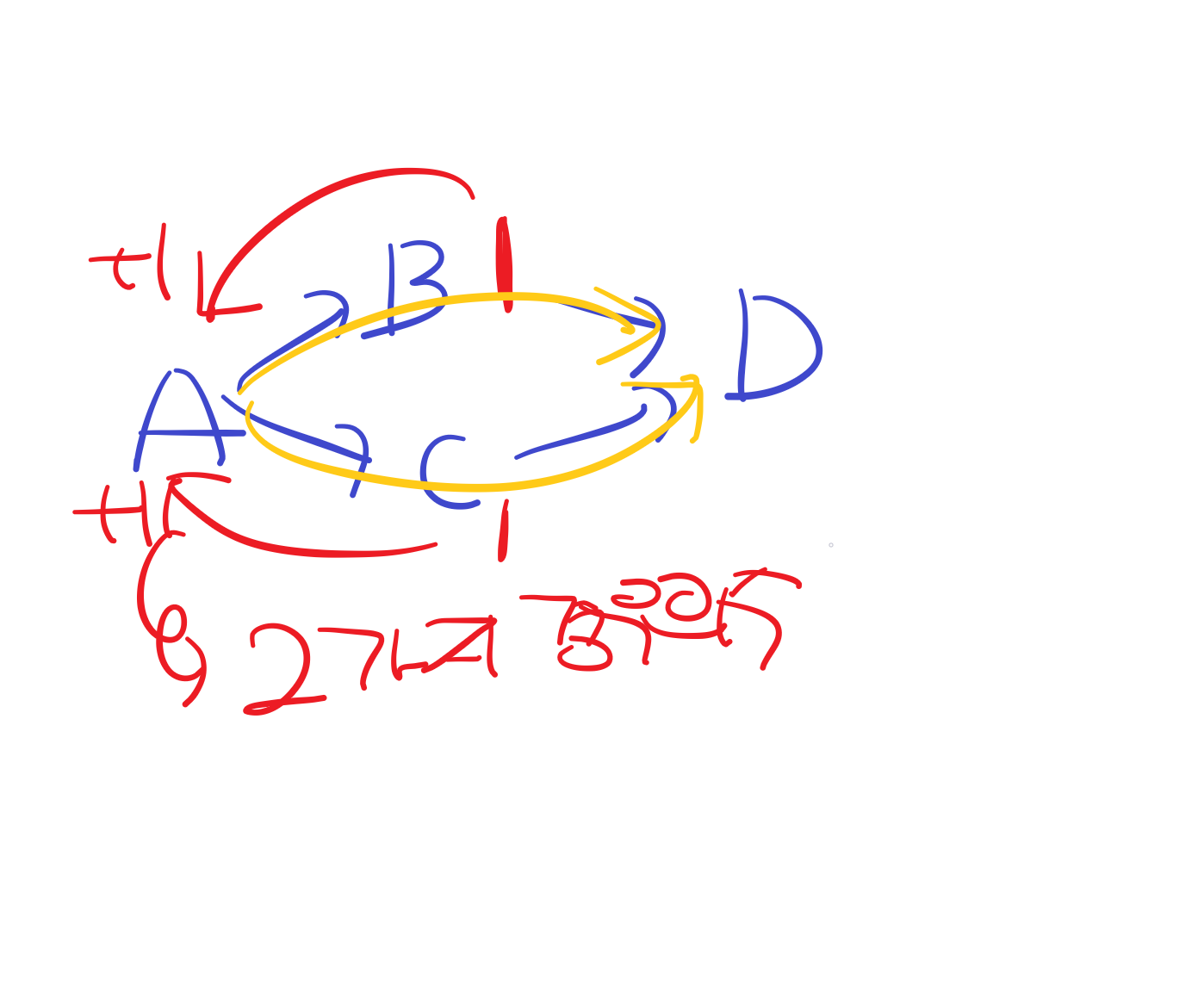A부터 D까지 가는 경우의 수는 2가지입니다.

이는 어떻게 계산될까요?

A로부터 연결되어있는 노드는 총 2가지, B, C밖에 없습니다.

그래서 B와 C라는 2가지의 경우의 수를 더하게 됩니다.

이 경우의 수가 결국 마지막에 가서 D까지 간다면 해당 경우의 수는 1이라는 값을 갖고

그 값이 타고 타고 돌아와서 A에 합쳐져서 2가 되는 것입니다.

이는. 이 꼴과 닮아있죠? 2가지의 경우의 수를 "더한다." 라는 것이니까요.

	return go(idx + 1, sum + v[idx]) + go(idx + 1, sum);

또한 go라는 함수는 마지막에가서는

	if(idx == n){
		//cout << "SUM " << sum << "\n";
		return check(sum); 
	}

check함수를 통해 1 또는 0임을 반환합니다. 이러한 값들이 쌓여서 경우의수가 되는 것입니다.

아까 든 그림있죠?

그걸 좀 바꿔볼까요?

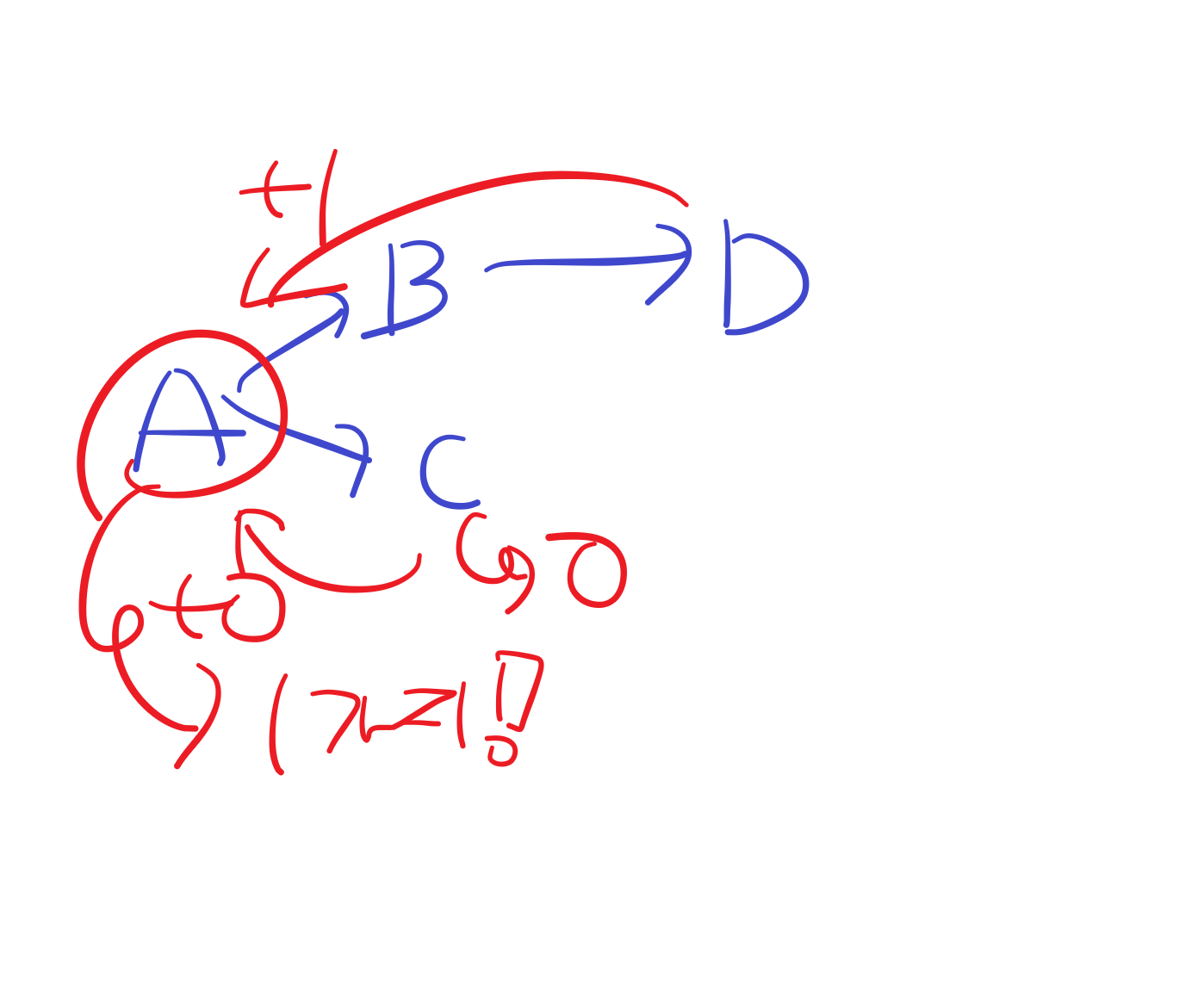만약 c로부터 d까지 가는 경로가 없다면 총 경우의 수는 1가지가 됩니다.

그러나 이를 계산하는 코드를 작성할 때는 그저 a와 연결된 b, c 라는 정점을 모두 탐색하는 코드로 구축할 수 밖에 없습니다.

그리고 c라는 정점에서 d까지 가는 게 없다면 0을 반환하게 만들고 b라는 정점에서 d까지 가는 경로가 있다면 1이라는 것을 반환하게 만들어 해당 값들을 합쳐서 a라는 정점에서 시작해서 d까지 가는 경우의 수를 구하게 하면 되는 것이죠.

Q4. 강의 영상을 보고나서 특정 숫자에 대해 포함한 경우, 포함하지 않는 경우를 활용하여 해결해야 한다고 표면적인 이해만 완료한 상태입니다. 하지만, 문제 해결을 위한 설계 부분에서 이해가 부족한 것 같습니다. 문제 해결을 위한 설계 부분에 대해서 좀 더 깊은 설명을 부탁드려도 될까요? 재귀함수 진짜 때려 잡고 싶습니다..

좋습니다.

이 문제는 크게 3가지만 생각하면 되요

1. 배열 탐색

idx가 증가하면서 즉, idx + 1을 해가며 배열을 탐색하죠?

물론..

문제를 보면

"몇 개를 골라 숫자의 합"

이라는 말이 있고 그냥 무작위로 탐색할수도 있지만

순서를 정해 쉽게 순회하는게 좋겠죠?

자 그러면 idx + 1을 해가며 요소들을 탐색해야 합니다.

2. 경우의 수 생각

자, 배열을 탐색하면서 어떤 경우의 수가 있죠?

해당 요소를 포함하냐, 또는 포함하지 않는 것.

두가지 밖에 없죠?

그러면 그 부분을 코드로 구현하는 것입니다.

포함하냐는 것은 굳이 배열을 쓸 필요는 없습니다. 이 문제는 해당 집합의 합을 기반으로 소수인지만 확인하면 되니까요. 그래서 sum + 해당idx값 또는 그냥 sum 으로 나눠지게 됩니다.

	return go(idx + 1, sum + v[idx]) + go(idx + 1, sum);

3. 확인

그리고 쌓아놓은 집합을 기반으로 마지막에 가서 확인한다!! = 기저사례 설정

이렇게 되는 것이죠.

보통의 완탐은 마지막에 확인하면 풀립니다.

즉, 기저사례부분에 어떠한 조건이 유효한지를 넣어 해당 값들이 쌓아서 값들을 만들면 되는 것입니다. 이 문제의 조건을 보면 소수가 되어야 합니다. 즉, 마지막에 소수를 체크하고 0 또는 1이라는 값을 통해 해당 집합이 유효한지를 파악하고 이 값들을 쌓아서 경우의 수를 만들면 되는 것입니다.

재귀함수는 어떻게 퍼져나가고 그리고 그 값들이 어떻게 누적되어 어떠한 값으로 만들어지는 지만 감을 잡으면 쉽습니다. 그리고 너무 어렵게 생각하지 말고 이 idx에서 어떻게 해야할까? 이부분만 집중해서 생각하시면 됩니다.

또 질문 있으시면 언제든지 질문 부탁드립니다.

좋은 수강평과 별점 5점은 제가 큰 힘이 됩니다. :)

감사합니다.

강사 큰돌 올림.