순열을 재귀함수로 구현했을 때의 장점

안녕하세요 승훈님 ㅎㅎ

next_permutation을 통해 순열을 구현하고자 할 때, 순열을 적용하고자 하는 컨테이너가 정렬되어 있어야 한다는 전제 조건이 필요합니다. 따라서 우리가 어떤 알고리듬 문제를 next_permutation으로 해결하고자 할 때, 평균적으로 O(nlogn)의 성능이 필요합니다. 반면, 재귀 함수로 순열을 구현하는 경우 순열을 적용하고자 하는 컨테이너의 순서와 상관없이 순열을 바로 적용할 수 있습니다. 그렇다면, 재귀 함수를 통해 순열을 구현하는 방법을 선호하는 것이 더 좋지 않을까요? 물론, 재귀 함수를 처리하는 데 드는 비용이 정렬을 처리하는 데 드는 비용보다 높다면 next_permutation 함수를 사용하는 것이 더 효율적이라고 생각합니다!

네 sort 는 O(nlogn)이 무조건 필요하죠. 날카로운 질문이네요. ㅎㅎ

( 이런 비판적으로 생각하는 자세는 정말 좋습니다.ㅎㅎ)

결론부터 말씀드리면, 성능으로 따졌을 때 재귀함수가 더 좋지만, 코테에서는 무관하며, 코테에서는 next_permutation을 쓰는게 보통은 더 좋습니다.

왜 그럴까요?

자, nP2이상인 경우 보통 O(n^2) 이상의 시간복잡도가 필요합니다.

이런 공식을 가지니까요. ㅎㅎ

즉, 문제에서 순열을 내는 문제는 보통은 O(n^2) 이상의 시간복잡도는 허용하는 문제임이 자명합니다.

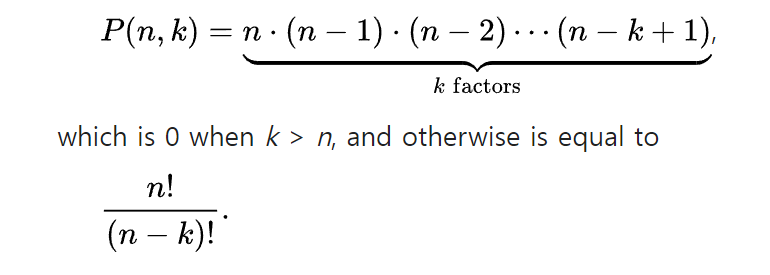
그렇기 때문에 O(n^2) 보다 낮은 수준의 O(nlogn)의 시간복잡도가 추가된다고 한들 문제를 푸는데 미치는 영향은 거의 없다고 보시면 됩니다.

또한, next_permutation이란 함수는 내부에서는 lexicographical_compare 를 기반으로 순열을 만듭니다. 해당 부분은 간단한 반복문으로 이루어져 있구요.

template <class InputIterator1, class InputIterator2>
  bool lexicographical_compare (InputIterator1 first1, InputIterator1 last1,
                                InputIterator2 first2, InputIterator2 last2)
{
  while (first1!=last1)
  {
    if (first2==last2 || *first2<*first1) return false;
    else if (*first1<*first2) return true;
    ++first1; ++first2;
  }
  return (first2!=last2);
}

따라서 보통 코테를 풀 때 순열이 필요한 경우에 next_permutation으로 하는게 좋습니다.

하지만!!

이거는 코테에서 그렇다는 것이구 성능상으로 봤을 때는 sort + next 보다는 재귀함수로 구축하는게 더 빠릅니다. 보통은 재귀함수를 호출하는데 드는 코스트가 더 크지만, next_permutation은 몇개중에 몇개를 뽑는다기 보다는 전체 배열을 계속해서 섞어서 순열을 무조건 만들어야 하기 때문입니다.

그렇다면 두개를 정확히 비교해볼까요?

sort + next_permutation과 재귀함수를 비교하는 벤치마킹을 시도해봤습니다. 원래는 n을 100만 이상으로 하는데 permutation 자체가 팩토리얼이기 때문에 n은 7 * 2 = 14 로 했습니다. (그 이상은 벤치마킹 자체가 안됩니다)

https://perfbench.com/

// ------------------------------------------------------------------------- //
// Welcome to Perfbench: online C++ code profiling tool.                     //
// Below is a short boilerplate to start with if you are familiar with API.  //
// Otherwise, use the main.cpp example or read the "help" and "api" tabs.    // 
// ------------------------------------------------------------------------- //

#include <bits/stdc++.h>
using namespace std; 
void makePermutation(int n, int r, int depth, vector<int> & v){
    if(r == depth){  
        return;
    }
    for(int i = depth; i < n; i++){
        swap(v[i], v[depth]);
        makePermutation(n, r, depth + 1, v);
        swap(v[i], v[depth]);
    }
    return; 
} 

void A(){
  vector<int> v;
  int n = 7;
  for(int i = 1; i < n; i++){
    v.push_back(i);
    v.push_back(n - i);
  }
  sort(v.begin(), v.end()); 
  while(next_permutation(v.begin(), v.end()));
}
 
void B(){
  vector<int> v;
  int n = 7;
  for(int i = 1; i < n; i++){
    v.push_back(i);
    v.push_back(n - i);
  }    
  makePermutation(n, n, 0, v);
}
void test_latency(size_t iteration) {  

  PROFILE_START("A"); 
  A();
  PROFILE_STOP("A");
  PROFILE_START("B");
  B();
  PROFILE_STOP("B");
}

int main() {
  const size_t warmups = 100;
  const size_t tests = 100;
 
  PROFILE_RUN_ALL(warmups, tests, 
    test_latency(__loop);
  );

  return 0;
}

앞의 그림처럼 B가 더 낮은 것을 볼 수 있습니다.

즉, 재귀함수가 더 빠릅니다. 그러나 코테에서 순열이 나온다는것은 어차피 O(n^2)이상의 시간을 허용하는 것이라 이와는 상관없이 next_permutation으로 구축해도 무방합니다.

또 질문 있으시면 언제든지 질문 부탁드립니다.

좋은 수강평과 별점 5점은 제가 큰 힘이 됩니다. :)

감사합니다.

강사 큰돌 올림.

인프런 커뮤니티 질문&답변