인프런 커뮤니티 질문&답변
[3.11] 4바이트 정수 범위에서 왜 유효숫자가 9개인지 모르겠습니다.
작성
·
389
1
-2,147,483,648에서 -2 자리는 모든 숫자 (-3, -4) 이런 건 안 되니까 정밀도로 보장할 수 없고 나머지는 정밀도로 보장이 된다고 하셨는데 -2 자리는 왜 정밀도로 보장할 수 없다는 건지 뭐가 안 된다는 건지 이해가 되지 않습니다. 그리고 정밀도로 보장한다 안 한다의 개념이 무엇인지 좀 더 명확하게 알고 싶습니다.
exponent를 저장할 때 음의 지수가 필요
- unsigned 형태로 저장을 하고 127을 빼기 8bit 정수는 0 ~ 255까지인데 -127을 하면 -127 ~ 128 범위의 숫자를 표현할 수 있기 때문
+) unsigned int 타입으로 저장을 할 때 모든 bit가 0이거나 1인 경우에는 다른 용도로 사용을 한다고 함
일반적으로 -126에서 128의 범위를 가짐
위 설명에서 이해 안 되는 점
1. 컴퓨터가 지수를 저장할 때 왜 음의 지수가 필요한지
2. 다른 용도라는 게 무엇을 말하는 건지
3. 앞에 음의 지수를 나타내는 방법 설명하실 때는 0~255 범위에서 -127을 하니까 -127~128 범위를 가진다고 하셨는데 왜 추가적으로 설명한 부분(모든 bit가 0이거나 1인 경우)에서는 -127~128이 아닌 -126~128의 범위를 가지는지답변 해주시면 감사하겠습니다.
답변 1
1
안녕하세요, 답변 도우미 Soobak 입니다.
질문 1) -2,147,483,648에서 -2 자리는 모든 숫자 (-3, -4) 이런 건 안 되니까 정밀도로 보장할 수 없고 나머지는 정밀도로 보장이 된다고 하셨는데 -2 자리는 왜 정밀도로 보장할 수 없다는 건지 뭐가 안 된다는 건지 이해가 되지 않습니다. 그리고 정밀도로 보장한다 안 한다의 개념이 무엇인지 좀 더 명확하게 알고 싶습니다.
: 정밀도를 보장한다는 것은 해당 자료형이 표현할 수 있는 값의 범위 내에서 모든 값을 정확하게 저장하고 연산할 수 있다는 것을 의미합니다.
예를 들어서, 32비트 int 자료형에서, 9자리 정밀도를 보장한다는 것은 최대 9자리 정수를 저장하고 계산할 때 오류나 문제가 없다는 것을 의미합니다.
또한, 32비트 int 자료형이 표현할 수 있는 값의 범위는 -2,147,483,648 부터 2,147,483,647 입니다.
해당 범위의 최대 절대값은 약 2.1 * 10^9 이므로, int 자료형에서 정밀도를 보장할 수 있는 자리수가 9자리인 것입니다.
말씀하신 -2 의 자리를 예시로 들어보면, -3,147,483,648 과 같이 -3 이 오는 경우에는 32비트 int 자료형이 표현할 수 있는 숫자의 범위를 벗어나기 때문에 정밀도를 보장하지 못하게 됩니다.
질문 2) exponent를 저장할 때 음의 지수가 필요 (중략) 위 설명에서 이해 안 되는 점
(1) 컴퓨터가 지수를 저장할 때 왜 음의 지수가 필요한지
: 부동 소수점 표현에서 작은 값을 표현하고 처리하기 위해 필요합니다.
지수가 음수인 경우, 해당 수는 2 의 음수 거듭제곱으로 표현된다는 것을 의미합니다.
한 번 쯤은 직접 계산해보시면 이해가 더 수월하실 것 같습니다.
예를 들어서, 지수가 -3 인 경우, 2^(-3) = 1 / 2^3 = 1 /8 = 0.125 로 표현이 됩니다. 이런 방식으로 매우 작은 수를 효과적으로 표현할 수 있습니다.
(2) 다른 용도라는 게 무엇을 말하는 건지
: 이어지는 강의인 3.12 부동소수점형의 한계 에서 예시들을 접하시게 되는데요, 무한대를 나타내는 INF (Infinity) , 수치적으로 표현할 수 없거나 정의되지 않는 값인 NaN (Not a Number) 등을 표현하기 위한 용도로 사용됩니다.
구체적으로 설명드려보면, 지수 부분이 0 , 1 일 때에 대해서는 다음과 같은 용도로 사용됩니다.
지수 값이
0인 경우 :i. 가수가
0인 경우 :sign부호에 따라서+0또는-0을 표현하는 용도ii. 가수가
0이 아닌 경우 : '비정규화된 수,(Denormalized numbers)' 로 매우 작은 부동 소수점 값을 표현할 수 있도록 돕는 용도지수 값이
255인 경우:
i. 가수가0인 경우 :sign부호에 따라서, 양의 무한대+INF또는 음의 무한대-INF를 나타내는 용도
ii. 가수가0이 아닌 경우 :NaN(Not a Number) 을 나타내기 위한 용도.
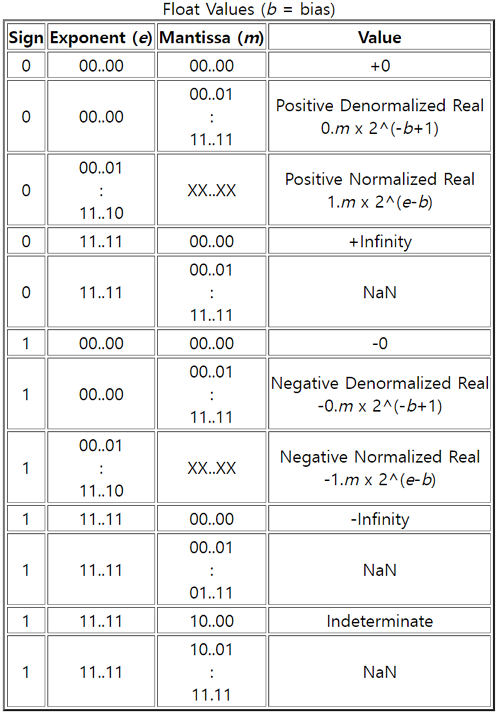
출처 - IEEE Standard 754 Floating Point Numbers (링크)
(3) 앞에 음의 지수를 나타내는 방법 설명하실 때는 0~255 범위에서 -127을 하니까 -127~128 범위를 가진다고 하셨는데 왜 추가적으로 설명한 부분(모든 bit가 0이거나 1인 경우)에서는 -127~128이 아닌 -126~128의 범위를 가지는지
: 바로 윗 질문에 대한 답변에서 설명드린 것처럼 지수부가 표현할 수 있는 숫자의 범위 내에서 '다른 용도' 로 사용하는 경우가 있기 때문에 범위가 줄어듭니다.
안녕하세요, 답변 도우미 Soobak 입니다.
질문) 답변 3번에서 -127~128이 아닌 -126~128 범위를 가지게 되는 건 범위가 줄어든 게 아니라 늘어난 것 아닌가요?
: 아닙니다. 숫자의 범위는 다음과 같이 계산됩니다.범위 = 최댓값 - 최솟값
- -127 ~ 128 의 범위는 128 - (-127) = 255 입니다.
- -126 ~ 128 의 범위는 128 - (-126) = 254 입니다.
따라서, 범위가 줄어든 것이 맞습니다.
지수부의 일부가 다른 용도로 사용하는 경우에 대한 예시에 위의 답변에서 표와 추가 자료링크와 함께 충분히 답변드린 것 같습니다. 링크 글도 한 번 읽어보시면 더 이해가 수월하실 것 같습니다. 보다 자세한 내용은 더 깊이가 있는 내용이며, 현재 문법을 공부하시는 단계에서 학습하시기에는 어려운 내용이라고 생각됩니다. 또한, float 자료형의 지수부/가수부 등의 경우의 수 및 예시는 구현 방식에 따라서 내부적으로 다릅니다. 따라서, float 자료형의 지수부와 가수부의 경우 별 구현 방식의 모든 케이스에 대한 설명을 모두 드리기에는 한계가 있는 것 같습니다.
현재 문법을 학습하시는 과정에서 강의 3.11 부동소수점형 과 3.12 부동소수점형의 한계 에서 핵심이 되는 내용 중 하나인 "지수부의 범위 중 INF , NaN 등 다른 용도로 사용하는 경우가 있다" 에 초점을 맞추어서 학습을 이어나가시는 것을 권장드립니다.

답변 3번에서 -127~128이 아닌 -126~128 범위를 가지게 되는 건 범위가 줄어든 게 아니라 늘어난 것 아닌가요? 다른 용도로 사용하는 경우에 줄어든 범위가 어떻게 되는지(ex. -126~127 이렇게 숫자로) 알려주시면 감사하겠습니다.