인프런 커뮤니티 질문&답변
3-G번 질문있습니다.
작성
·
383
1
- 학습 관련 질문을 남겨주세요. 상세히 작성하면 더 좋아요!
- 먼저 유사한 질문이 있었는지 검색해보세요.
- 서로 예의를 지키며 존중하는 문화를 만들어가요.
- 잠깐! 인프런 서비스 운영 관련 문의는 1:1 문의하기를 이용해주세요.
3-G 문제에서 정점에 이미 방문한 경우
(현 정점 거리 +1 == 다음 정점 거리) 인 경우만 체크해주는데
(현 정점 거리 +1 < 다음 정점 거리) 인 경우는 존재하지 않아서 체크하지 않는 건가요??
궁금해서 질문드립니다. 감사합니다.
답변 3
0
0
안녕하세요 mim님 ㅎㅎ
(현 정점 거리 +1 < 다음 정점 거리) 인 경우는 존재하지 않아서 체크하지 않는 건가요??
>> 존재하지 않습니다.(수정 :: 밑 댓글에 서술)
if (!visited[next]) {
q.push(next);
visited[next] = visited[now] + 1;
cnt[next] += cnt[now];
} else if (visited[next] == visited[now] + 1) {
cnt[next] += cnt[now];
}이부분을 말씀하시는거죠? 여기서 visited[next] == visited[now] + 1 일 때 cnt += cnt[now]요.
이건 뭐냐면 최단거리로 가는데. 똑같은 경우의 수가 하나 더를!! 찾은 경우입니다.
이 문제의 경우
가장 빠른 시간으로 찾는 방법이 몇 가지 인지 구하는 프로그램을 작성하시오.
즉, 방법을 몇가지인지를 찾는 문제죠?
자 2초만에 a라는 정점을 오는 경우의 수가 있습니다. 그러면 a라는 정점은 visited가 되어있겠죠? 2로 색칠되어있을 겁니다.
근데 또 갑자기 b에서 a로 가는데 2초만에 a라는 정점을 오는 경우의 수가 생기겠죠. 이 경우
visited[b] + 1 == visited[a]라는 조건이 성립하게 됩니다.
그래서 저런식으로 해서 최단거리인데!! 해당 방법의 수를 더하는 로직을 완성시킬 수 있는 것이죠.
감사합니다.
아 답변 변경하겠습니다. ㅎㅎ;
(현 정점 거리 +1 < 다음 정점 거리) 인 경우는 존재하지 않아서 체크하지 않는 건가요??
>> 해당부분은 존재하지 않습니다.
이는 가중치가 같은 그래프를 BFS로 탐색해서 그런데요. BFS로 가중치가 같은 그래프를 탐색하게 되었을 때 방문되는 정점은 최단거리가 됩니다. 이 문제는 +1, -1, * 2든 1초가 걸리는 가중치가 같은 그래프입니다. 따라서 BFS로 방문하는 정점은 최단거리가 됩니다.
지금 보시면
1에서 2로 가는 경우 1 + 1을 통해 2를 2초만에 가는게 가장 빠른 경우의 수죠? 그 다음 * 2로도 갈 수 있기 때문에 경우의 수인 cnt가 +가 됩니다.
1에서 2로 가는 수중 이보다 더 빠른 경우의 수는 없습니다.
해당 부분 그림으로 그려봤는데요.
참고 부탁드립니다.
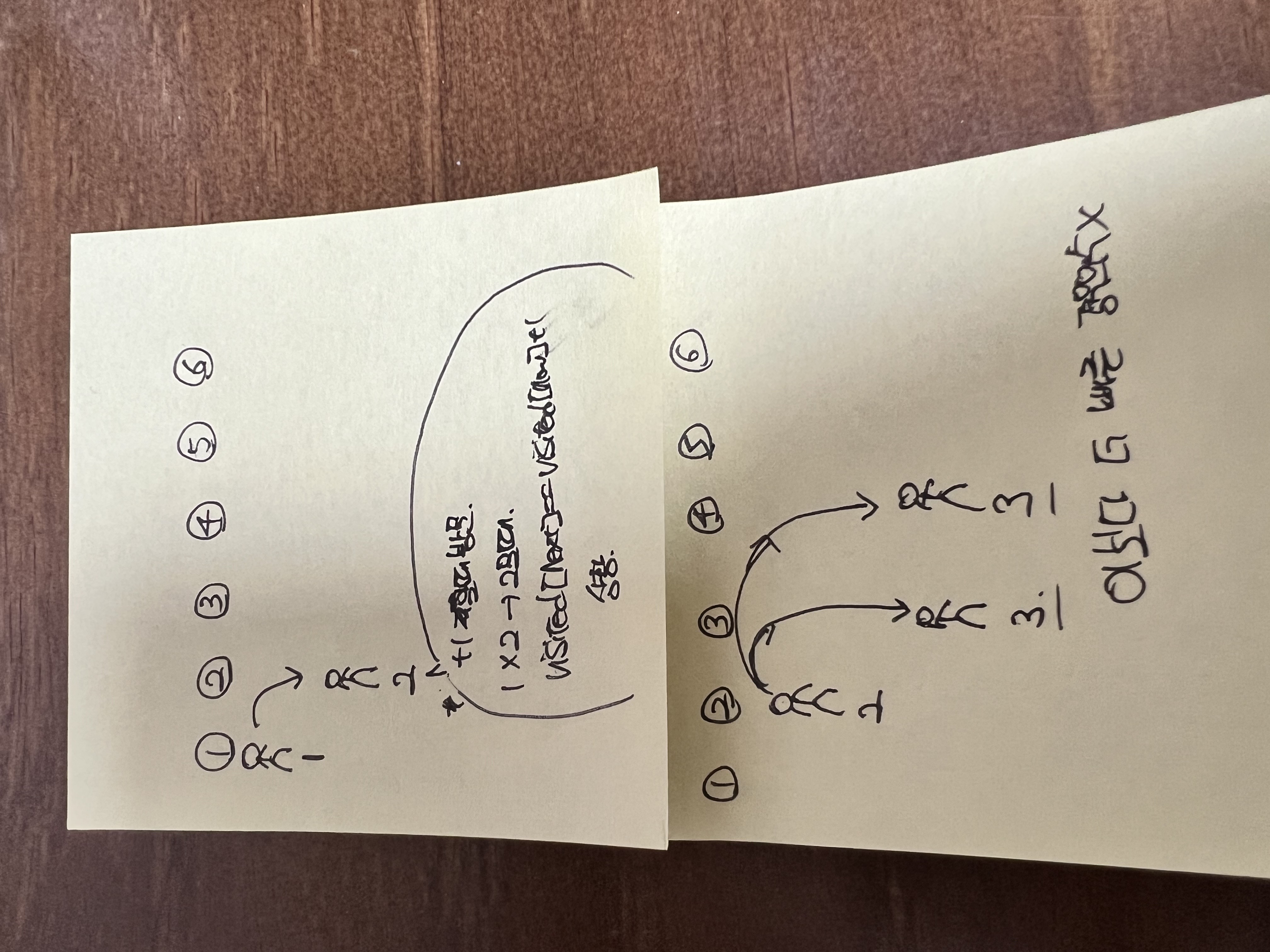
0

친절한 답변 감사합니다.
그런데 답변해주신 것처럼 visited[next] > visited[now] + 1 이 존재한다면
기존에 visited[next]에 저장해둔 시간보다 next 정점으로 가는 더 빠른 루트가 존재한다는 거
아닌가요?? 만약 존재한다면 값을 업데이트 해줘야 할 것 같다는 생각이 들어서 질문드립니다.