인프런 커뮤니티 질문&답변
3-B 강의를 보고 시간복잡도와 관련하여 질문드립니다
해결된 질문
작성
·
350
1
안녕하세요 강의 잘보고 있습니다.
시간복잡도에 대해 궁금한 부분이 있어 질문드립니다.
2주차 개념강의에서 BFS의 시간복잡도는 인접행렬의 경우 V^2라고 배웠습니다.
3-B 문제의 경우 최대 50*50배열이므로 최악의 경우 만약 모든 배열이 Land라면 V가 2500이 됩니다.
for문을 통해 모든 배열을 탐색하면서 && Land에 대해 BFS를 한다면 최악의 경우 2500*2500*2500이라는 계산이 나왔습니다.
천만이 넘는 수치인대요
강의에서 천만이 넘지 않는다면 완전탐색으로 해보고 아니면 다른 방법을 시도래보라고(?) 배웠던 것 같아 문의드립니다.
애매하게 넘는 수준이라면 일단 시도해보아도 되는 것일까요? 물론 뒤의 강의들을 배우면 시간복잡도가 더 낮은 방법들이 있다고 배웠습니다만, 시간이 정해져있는 시험의 경우 일단 시도했다가 안 되면 어떻게 하지? 하는 괜한 맘이 생겨서요
아니면 제가 시간복잡도 계산 방법에 대해 잘못 알고 있는 것인지 질문드립니다.
감사합니다.
답변 4
1
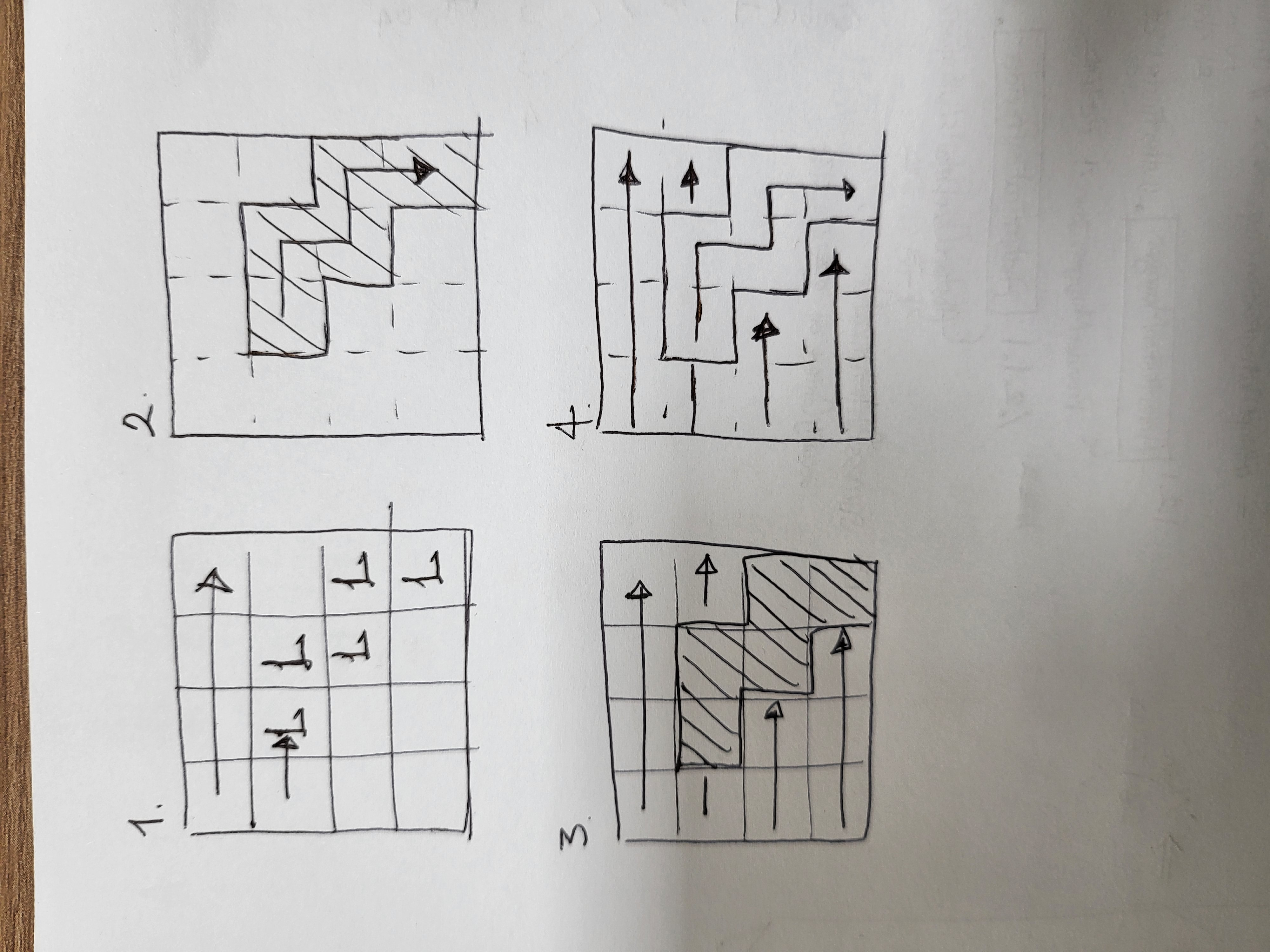
위 그림을 보시면
그림1 에서 이중for문을 돌고 if(visited[i][j] == false && map[i][j] == 'L') 일 때만 bfs/dfs를 진행하게 하면
그림2 처럼 (1, 1)좌표부터 연결된 모든 L지점을 탐색합니다.
그림3 은 그림2에서 탐색을 마친 후 다시 이중for문을 마저 수행하는 것을 그린 것인데요
visited[i][j] = true인 지점들은 무시하게 됩니다.
그림4. 결국 모든 맵의 지점을 순회하는 셈인데요,
위 설명을 이해하셨다면
모든 맵이 L 인 상황에서는 (0, 0)에서 bfs시작하여 모든 위치들을 탐색하고 이후 남은 이중for문의 턴들은 if문의 visited[i][j] 덕분에 더는 연산이 발생하지 않습니다.
위 첫 밑줄에서는 연산이 50*50 발생
두번째 밑줄에서는 질문자님의 2500번 for문을 수행하다는 예상과 달리 0회 발생합니다
정리하자면,
정점의 시간복잡도는 정점갯수^2 인데 반해
지도(맵)의 시간복잡도는 지도크기인 O(가로 x 세로 x 맵을 훑는 횟수) 라고 정리할 수 있습니다.
한 번 탐색으로 끝나는 위와같은 문제면 맵을 훑는 횟수 는 1회겠죠
헉,,, 그림까지 그려가며 자세히 설명해주셔 감사합니다.
확실히 1천만 이하로 나오겠습니다
굳이 시간복잡도를 계산한다고 했을 때도 말씀해주신 '맵을 훑는 횟수'는 해당 지도의 커넥티드 컴포넌트들의 개수(실행될 bfs의 횟수)에 따라 각 커넥티드 컴포넌트를 구성하는 노드들로 인한 인접행렬의 시간복잡도(실행된 bfs에 대한 시간복잡도) 정도?겠네요.
자세하게 설명해주셔서 다시 한 번 감사합니다!
백준 보물섬 같은 문제에서 인접행렬 언급은 적절치 않은 것 같아요.
맵(지도)이라는 이차원배열은 문제마다 가로와 세로의 길이가 같지 않을 수 있습니다.
즉, 사각행렬일 뿐이지 항상 정사각행렬이 아닙니다.
따라서 "섬 5개, 섬 사이에 다리가 놓여있는 정보가 있는 문제"에서 섬에 번호를 부여하고
인접행렬 , 인접리스트을 이용하여 문제를 푸는건 적절하다고 생각이 듭니다.
위와 같은 맵문제에서는 사각행렬인 이차원배열을 사용하시면 됩니다.
마지막으로,
맵을 훑는 횟수는 문제상황에 따라 필요하면 모든 visited[i][j] 를 0 으로 하고 다시 전 맵을 탐색해야 될 수 도 있잖아요. 그런 상황을 고려했던 거에요. 보물섬에서 'L'이 모여있는 집단의 갯수(대륙의 갯수)와는 관련없고요. 오히려 문제그림에 나와있는 대륙들은 맵을 1회 훑을 때 모두 스캔하는 걸요.
1
위 문제는 지도 이고
블로그에서 선생님께서 설명하신 내용은 정점 입니다.
지도의 경우 시간복잡도와 공간복잡도가 맵의 싸이즈 O(가로 * 세로) 만큼 나오지 않을까요?
따라서 지도 를 전체 한 번 훑는데 드는 연산은 최대 50 * 50 번으로 계산될 것같습니다.
답변 감사합니다.
말씀해주신대로 위의 문제는 지도이고 선생님께서 말씀하신 bfs 시간복잡도의 내용은 정점에 대한 내용입니다
하지만 문제에서는
for(지도의 y축 탐색){
for(지도의 x축 탐색){
조건에 맞으면 bfs 탐색
}
}
이런 형태라서 지도 전체가 land, 즉 지도 전체를 훑게 된다면 for문으로 50*50번의 연산에 중첩하여 bfs탐색(정점*정점 시간복잡도, 여기서 각 정점은 전체가 land이니 50*50개)를 가지니 시간복잡도가 1천만을 넘는 것 아닌가? 하는 의문이었습니다.
제가 시간복잡도 계산하는 방법이 잘못된 것 같은 의문도 드네요
1
안녕하세요. namk님 ㅎㅎ
강의에서 천만이 넘지 않는다면 완전탐색으로 해보고 아니면 다른 방법을 시도래보라고(?) 배웠던 것 같아 문의드립니다.
>> 시간복잡도 설명할 때 먼저 "문제에 따라 다르지만" 이라면서 보통 몇천만, 1억이면 좀 높다라고 말씀을 드렸습니다. namk님 말씀 처럼 천만의 경우 안되기도 합니다만 천만이면 일단 시도해주세요.
애매하게 넘는 수준이라면 일단 시도해보아도 되는 것일까요? 물론 뒤의 강의들을 배우면 시간복잡도가 더 낮은 방법들이 있다고 배웠습니다만, 시간이 정해져있는 시험의 경우 일단 시도했다가 안 되면 어떻게 하지? 하는 괜한 맘이 생겨서요
>> 그런맘이 생기시는 것은 이해하지만 어쩔 수 없다고 생각해요. 저 또한 코테나 대회를 나가서 문제를 풀 때 "한번에" 푸는 경우는 있긴 하지만 매번 그렇게 "한번에"푸는 경우는 없습니다. 지금은 일단 시도해본다고 생각해주세요. 한 8주차까지 가게 되면 이렇게 될겁니다. 문제를 보시고 완탐? DP? 그리디? 아 완탐으로 되겠네 이런 생각의 로직이 매끄럽게 흘러가면서조금 더 체계적으로 문제의 해설방법을 생각해서 푸시게 될겁니다. 그러나 뭐든간에 한번에 문제를 풀면 베스트긴 하나 1 ~ 2번 정도의 시도로 푼다는 것이 일반적이다라는 생각은 가지셔야해요.
또 질문 있으시면 언제든지 질문 부탁드립니다.
감사합니다.
강사 큰돌 올림.
답변 감사합니다!
ps (이 영역은 대댓글에 나중에 덧붙여진 내용이지만 새로 생각하게 된 의문이 큰돌님의 질문 읽는 시간을 줄일 것 같아 앞으로 옮기게 되었습니다.)
추가로 다른 질문들을 살펴보면서 유사한 질문을 발견하였습니다.
저는 고유좌표가 2500개이니 막연히 정점을 2500개라고 생각했는데요.
다른 질문과 답변을 보면서 생각해보니 인접행렬은 각 노드간의 연결성을 행렬로 나타낸 것이니깐 50*50 행렬지도의 모든 구성이 Land인 경우. V가 2500개인 인접행렬이 아니라, V가 2500개고 간선이 각 정점에 대해 4방위로 4개씩 있다고 (대략적으로) 생각하여 2500*4 = 1만개.
즉 2500+1만을 BFS의 시간복잡도로 계산해야하나? 생각하게 되었습니다.
(이렇게 계산해도 지도 전체를 탐색하는 이중for문 50*50과 위에서 계산한 BFS의 시간복잡도 1.25만을 곱했을 때 1천만이 아닌 3천만을 넘기는 합니다.)
제가 생각하고 계산한 것이 맞는지, 혹 틀렸다면 실제 문제를 푸는 과정에서 BFS의 시간복잡도 계산을 어떻게 하는지 궁금합니다.
감사합니다.
답변해주신대로 애매하면 시도해보고, 강의도 완강하며 다양한 방법을 배우도록 하겠습니다. 감사합니다
추가로 여쭙는다면 이전 질문의 베이스가 되었던 의문은
해설코드는
for(지도의 y축 탐색){
for(지도의 x축 탐색){
조건에 맞으면 bfs 탐색
}
}
이렇게 진행되는대요.
y축이 최대 50, x축이 최대 50, 조건(여기서는 land)이 지도 전체라면 bfs가 탐색할 정점의 개수는 50*50
>> 전체 시간복잡도는 50*50*(50*50)^2 => 1억을 넘는 숫자
>> 최악의 경우 시간복잡도가 1천만이 넘는 것 같은데 괜찮은걸까? 하는 의문이었습니다.
큰돌님의 답변도, 밑에 추가로 답변 주신 분의 내용도 제가 계산하는 시간복잡도가 틀린 것 같다는 의구심을 갖게 하는대요. 시간복잡도 계산이 이런 식으로 진행되는 것이 아닌지, 올바른 시간복잡도 계산은 어떻게 하는 것인지 궁금합니다 ㅠㅠ
감사합니다.

선생님 답변 감사합니다~
질문자분께서 혼란스럽지 말라고 추가로 말씀드리면
최대시간복잡도계산은 아래와 같습니다.
선생님께서 알려준 값이 절대 인접행렬의 시간복잡도O(V^2) 계산하듯 2500^2 으로 나온 값이 아닙니다.
모범답안 기준)
BFS로 연결된 'L' 지점들 모두 탐색할 때 주어진 맵이 최악으로 모든 위치가 'L' 이면
맵 크기만큼 탐색한다. 따라서
가로 x 세로= 50 x 50 = 2500번이중for문의 if문에서
visited[i][j] == true체크를 하지 않는 특징 때문에 모든 이중for문의 턴마다 BFS를 진행한다. 이중for문의 반복횟수는i < n, j < m으로 최대2500번따라서
최대연산횟수 = 2500 * 2500 번