인프런 커뮤니티 질문&답변
1. Kaggle House Prices 예제에서 R2 와 Coefficent 값 질문
작성
·
194
0
답변 3
0
1. 하지만 log 변환한 값으로 lr, ridge, lasso 세가지를 돌렸을 때는 하기와 같이 lr의 경우는 coef 값이 제대로 나오지 않고, lasso의 경우는 대부분 0.0 값이 나오는데, 또 code가 잘못된 것인지, 아니면 이렇게 값이 이상하게 나올 경우는 하이퍼파라미터 튜닝을 통해서 성능을 올려야할 케이스에 해당이 될까요?
=> 이거는 작성하신 코드를 보지 않고는 알 수가 없을 것 같습니다. 여기에 작성한 전체 코드를 올려봐 주십시요. 그리고 log변환을 했다는 것이 타겟값을 했다는 건지 피처값을 했다는 것지요?
--> 네, Object feature는 Drop 하고, Object 타입이 아닌 feature 에 대해서만 하기와 같이 col_x_names 에 넣어 Standard Scaling 을 하였고, Target 값인 SalePrice 에 대해서만 log1p 로 로그 변환하였습니다.
2. lr의 경우도, 일부가 coef값이 0.0 으로 나오는데, lr도 하이퍼파라미터튜닝과 같이 성능을 높일 수 있는 방법이 있을까요?
=>LinearRegression 클래스는 하이퍼파라미터라 할만한 초기화 값이 없습니다만, 굳이 찾자면, fit_intercept(절편 반영 여부) 정도 될 것 같습니다. LinearRegression은 보다는 Ridge, Lasso 사용을 권장드립니다.
--> 네 설명 감사합니다!!
3. 추가로 log1p 한 이후 Model 완료 후 다시 expm1() 함수로 복원할 때 코드도 어떻게 쓰는 것이 맞는지 알려주신다면 너무 감사하겠습니다.
=> 분류 실습 2: 신용카드 사기 예측 실습 - 03 강의의 8분 50초 정도의 내용을 확인해 보시면 좋을 것 같습니다. 만약에 해당 내용을 보셨는데도 이해가 안되셨다면 어느 부분이 이해가 안되신건지 좀 더 자세하게 기재 부탁드립니다.
--> 네, 제가 해당 강의는 아직 못들었는데, 이해 안되면 문의 드리겠습니다.
이렇게 일일이 설명 자세히 해주셔서 너무 감사합니다!!
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
house_df_org = pd.read_csv('house_price.csv')
house_df = house_df_org.copy()
house_df.head(3)
#Object feature drop
house_df.drop(['MSZoning', 'LotFrontage', 'Street','Alley','LotShape','LandContour','Utilities',
'LotConfig','LandSlope', 'Neighborhood', 'Condition1', 'Condition2','BldgType','HouseStyle',
'RoofStyle','RoofMatl', 'Exterior1st', 'Exterior2nd', 'MasVnrType','ExterQual','ExterCond',
'Foundation','BsmtQual', 'BsmtCond', 'BsmtExposure', 'BsmtFinType1','BsmtFinType2',
'Heating', 'HeatingQC', 'CentralAir','Electrical','KitchenQual','Functional','FireplaceQu','GarageType', 'GarageFinish', 'GarageQual','GarageCond',
'PavedDrive','PoolQC','Fence','MiscFeature', 'SaleType','SaleCondition','Id'], axis=1 , inplace=True)
# Null 값 평균값으로 대체
house_df.fillna(house_df.mean(),inplace=True)
col_x_names = ['MSSubClass','LotArea','OverallQual','OverallCond','YearBuilt','YearRemodAdd',
'MasVnrArea','BsmtFinSF1','BsmtFinSF2','BsmtUnfSF','TotalBsmtSF','1stFlrSF','2ndFlrSF',
'LowQualFinSF','GrLivArea','BsmtFullBath','BsmtHalfBath','FullBath','HalfBath','BedroomAbvGr',
'KitchenAbvGr','TotRmsAbvGrd','Fireplaces','GarageYrBlt','GarageCars','GarageArea',
'WoodDeckSF','OpenPorchSF','EnclosedPorch','3SsnPorch','ScreenPorch','PoolArea','MiscVal',
'MoSold','YrSold']
# Feature 별로 range차이가 크기 때문에 StandardScaler 처리 해줌
from sklearn.preprocessing import StandardScaler
import pandas as pd
col_x_names = ['MSSubClass','LotArea','OverallQual','OverallCond','YearBuilt','YearRemodAdd',
'MasVnrArea','BsmtFinSF1','BsmtFinSF2','BsmtUnfSF','TotalBsmtSF','1stFlrSF','2ndFlrSF',
'LowQualFinSF','GrLivArea','BsmtFullBath','BsmtHalfBath','FullBath','HalfBath','BedroomAbvGr',
'KitchenAbvGr','TotRmsAbvGrd','Fireplaces','GarageYrBlt','GarageCars','GarageArea',
'WoodDeckSF','OpenPorchSF','EnclosedPorch','3SsnPorch','ScreenPorch','PoolArea','MiscVal',
'MoSold','YrSold']
scaler = StandardScaler()
house_scaled_x = house_df[col_x_names]
scaler.fit(house_scaled_x)
house_scaled_x = scaler.transform(house_scaled_x)
#transform()시 scale 변환된 데이터 셋이 numpy ndarry로 반환되어 이를 DataFrame으로 변환
house_scaled_x = pd.DataFrame(data=house_scaled_x, columns=col_x_names)
print('mean of features')
print(house_scaled_x.mean())
print('\n variance of features')
print(house_scaled_x.var())
house_scaled_x
# 로그변환
original_SalePrice = house_df['SalePrice']
house_df['SalePrice'] = np.log1p(house_df['SalePrice'])
# R2 확인
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.metrics import mean_squared_error, r2_score
y_target = house_df['SalePrice']
X_data = house_scaled_x
X_train, X_test, y_train, y_test = train_test_split(X_data, y_target, test_size=0.2, random_state=156)
#선형회귀 OLS 로 학습/예측/평가 수행
lr_reg = LinearRegression()
lr_reg.fit(X_train, y_train)
y_preds = lr_reg.predict(X_test)
mse = mean_squared_error(y_test, y_preds)
rmse = np.sqrt(mse)
print('lr Variance score : {0: .7f}'.format(r2_score(y_test, y_preds)))
ridge_reg = Ridge()
ridge_reg.fit(X_train, y_train)
y_preds = ridge_reg.predict(X_test)
mse = mean_squared_error(y_test, y_preds)
rmse = np.sqrt(mse)
print('ridge Variance score : {0: .7f}'.format(r2_score(y_test, y_preds)))
lasso_reg = Lasso()
lasso_reg.fit(X_train, y_train)
y_preds = lasso_reg.predict(X_test)
mse = mean_squared_error(y_test, y_preds)
rmse = np.sqrt(mse)
print('lasso_reg Variance score : {0: .7f}'.format(r2_score(y_test, y_preds)))
# RMSE
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.metrics import mean_squared_error, r2_score
# 학습이 완료된 모델을 인자로 받아서 테스트 데이터로 예측하고 RMSE를 계산
def get_rmse(model):
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
print(model.__class__.__name__, 'RMSE:',np.round(rmse, 7))
return rmse
#여러 모델들을 list 형태로 인자로 받아서 개별 모델들의 RMSE 를 list 로 반환
def get_rmses(models):
rmses = []
for model in models:
rmse = get_rmse(model)
rmses.append(rmse)
return rmses
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.metrics import mean_squared_error, r2_score
y_target = house_df['SalePrice']
X_data = house_scaled_x
X_train, X_test, y_train, y_test = train_test_split(X_data, y_target, test_size=0.2, random_state=156)
#선형회귀 OLS 로 학습/예측/평가 수행
lr_reg = LinearRegression()
lr_reg.fit(X_train, y_train)
ridge_reg = Ridge()
ridge_reg.fit(X_train, y_train)
lasso_reg = Lasso()
lasso_reg.fit(X_train, y_train)
models = [lr_reg, ridge_reg, lasso_reg]
get_rmses(models)
# Coef 확인
coef = pd.Series(lr_reg.coef_, index=house_scaled_x.columns)
coef_high = coef.sort_values(ascending=False).head(20)
coef_high
coef = pd.Series(ridge_reg.coef_, index=house_scaled_x.columns)
coef_high = coef.sort_values(ascending=False).head(20)
coef_high
coef = pd.Series(lasso_reg.coef_, index=house_scaled_x.columns)
coef_high = coef.sort_values(ascending=False).head(20)
coef_high
#Coef 그래프
def get_top_bottom_coef(model):
#coef_속성을 기반으로 Series 객체를 생성. index는 컬럼명
coef = pd.Series(model.coef_, index=house_scaled_x.columns)
# +상위 10개, -하위 10개 coefficient 를 추출하여 반환.
coef_high = coef.sort_values(ascending=False).head(10)
coef_low = coef.sort_values(ascending=False).tail(10)
return coef_high, coef_low
def visualize_coefficient(models):
# 3개 회귀 모델의 시각화를 위해 3개의 컬럼을 가지는 subplot 생성
fig, axs = plt.subplots(figsize=(24, 10), nrows=1, ncols=3)
fig.tight_layout()
#입력인자로 받은 list 객체인 models 에서 차례로 model을 추출하여 회귀 계수 시각화
for i_num, model in enumerate(models):
#상위 10개, 하위 10개 회귀 계수를 구하고 이를 판다스 concat 으로 결합
coef_high, coef_low = get_top_bottom_coef(model)
coef_concat = pd.concat([coef_high, coef_low])
#순차적으로 ax subplot 에 barchar로 표현, 한화면에 표현하기 위해 tick label 위치와 font 크기 조정
axs[i_num].set_title(model.__class__.__name__+'Coeffiecents', size=25)
axs[i_num].tick_params(axis="y", direction="in", pad=-120)
for label in (axs[i_num].get_xticklabels() + axs[i_num].get_yticklabels()):
label.set_fontsize(22)
sns.barplot(x=coef_concat.values, y=coef_concat.index , ax=axs[i_num])
# 앞 예제에서 학습한 lr_reg, ridge_reg, lasso_reg 모델의 회귀 계수 시각화.
models = [lr_reg, ridge_reg, lasso_reg]
visualize_coefficient(models)0
강사님,
자세한 설명과 도움 너무 감사드립니다. 제 코드에 문제가 있었던 것이 맞는 것같습니다.
추가질문 여기에 드려도 될지 모르겠습니다.
저는 데이터 셋에서 object 피처는 다 drop 하고,
log변환하지 않은 SalePrice 값으로 lr, ridge, lasso를 돌려보니 RMSE, R2 값에 각각 큰 차이는 나지 않고, 아주 미세한 차이만 납니다.
하지만 log 변환한 값으로 lr, ridge, lasso 세가지를 돌렸을 때는 하기와 같이 lr의 경우는 coef 값이 제대로 나오지 않고, lasso의 경우는 대부분 0.0 값이 나오는데, 또 code가 잘못된 것인지, 아니면 이렇게 값이 이상하게 나올 경우는 하이퍼파라미터 튜닝을 통해서 성능을 올려야할 케이스에 해당이 될까요?
또한 lr의 경우도, 일부가 coef값이 0.0 으로 나오는데, lr도 하이퍼파라미터튜닝과 같이 성능을 높일 수 있는 방법이 있을까요?
추가로 log1p 한 이후 Model 완료 후 다시 expm1() 함수로 복원할 때 코드도 어떻게 쓰는 것이 맞는지 알려주신다면 너무 감사하겠습니다.
1. 하지만 log 변환한 값으로 lr, ridge, lasso 세가지를 돌렸을 때는 하기와 같이 lr의 경우는 coef 값이 제대로 나오지 않고, lasso의 경우는 대부분 0.0 값이 나오는데, 또 code가 잘못된 것인지, 아니면 이렇게 값이 이상하게 나올 경우는 하이퍼파라미터 튜닝을 통해서 성능을 올려야할 케이스에 해당이 될까요?
=> 이거는 작성하신 코드를 보지 않고는 알 수가 없을 것 같습니다. 여기에 작성한 전체 코드를 올려봐 주십시요. 그리고 log변환을 했다는 것이 타겟값을 했다는 건지 피처값을 했다는 것지요?
2. lr의 경우도, 일부가 coef값이 0.0 으로 나오는데, lr도 하이퍼파라미터튜닝과 같이 성능을 높일 수 있는 방법이 있을까요?
=>LinearRegression 클래스는 하이퍼파라미터라 할만한 초기화 값이 없습니다만, 굳이 찾자면, fit_intercept(절편 반영 여부) 정도 될 것 같습니다. LinearRegression은 보다는 Ridge, Lasso 사용을 권장드립니다.
3. 추가로 log1p 한 이후 Model 완료 후 다시 expm1() 함수로 복원할 때 코드도 어떻게 쓰는 것이 맞는지 알려주신다면 너무 감사하겠습니다.
=> 분류 실습 2: 신용카드 사기 예측 실습 - 03 강의의 8분 50초 정도의 내용을 확인해 보시면 좋을 것 같습니다. 만약에 해당 내용을 보셨는데도 이해가 안되셨다면 어느 부분이 이해가 안되신건지 좀 더 자세하게 기재 부탁드립니다.
0
안녕하십니까,
1. 뭔가 코드를 잘못 작성하신것 같습니다. 2개의 r2 score는 서로 다릅니다.
ridge_reg, lasso_reg를 학습 시킨 후 아래 코드로 다시 확인해 보시기 바랍니다.
print(cross_val_score(ridge_reg, X_features, y_target, scoring="r2", cv = 5))
print(cross_val_score(lasso_reg, X_features, y_target, scoring="r2", cv = 5))
2. 회귀 계수가 크다는 것은 아무래도 전체 피처 중에서 결정값을 예측하는데 상대적으로 영향도가 크다고 할 수 있습니다. 왜냐하면 예측 결정값은 회귀계수1* 피처1 + 회귀계수2*피처2 + ...... 와 같이 만들어 지기 때문입니다.
물론 스케일링을 적용하지 않은 학습 데이터라면 큰 회귀 계수가 결정값에 예측에 반드시 영향도가 크다고 할 수 없습니다. 왜냐하면 피처값 자체가 크면 회귀 계수가 작아도 결정값에 영향력이 커질 수 있기 때문입니다. 하지만 보통 선형회귀는 피처에 스케일링을 적용하므로 회귀 계수가 크면 결정값 예측하는데 상대적으로 영향도가 크다고 할 수 있습니다.

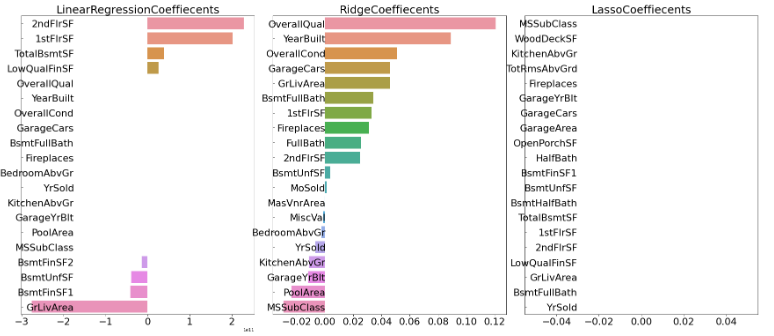
Lasso는 alpha값에 민감한 경우가 발생할 수 있습니다.
저렇게 많은 feature들의 회귀 계수값이 0이 되면 alpha값을 넣어 주십시요.
보통 0.1, 아니면 0.01 정도 설정후에 다시 회귀 계수를 확인해 보시면 됩니다.
lasso_reg = Lasso(alpha=0.01)