인프런 커뮤니티 질문&답변
random,randn(1000) 함수 질문드립니다
작성
·
756
답변 4
2
2
박조은
지식공유자
안녕하세요. 좋은 질문을 주셨네요.
In [1]:
import numpy as np
import pandas as pd
In [2]:
# 0부터 1사이의 균일 분포를 난수로 생성합니다.
rand = np.random.rand(100)
# 100개의 난수 중에 앞에서 10개의 난수만 슬라이싱으로 가져와서 미리보기를 합니다.
rand[:10]
Out[2]:
In [3]:
# 가우시안 분포(표준 정규분포)를 생성합니다.
randn = np.random.randn(100)
randn[:10]
Out[3]:
In [4]:
# 균일분포의 정수 난수를 생성합니다.
randint = np.random.randint(1, 10, 100)
randint[:10]
Out[4]:
In [5]:
# 위에서 만든 값을 데이터프레임으로 만들어서 비교를 합니다.
df = pd.DataFrame({"rand": rand, "randn": randn, "randint": randint})
In [6]:
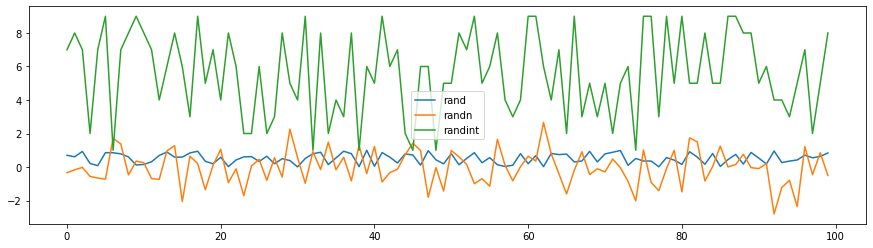
# 3가지 난수 생성방법으로 생성된 값을 비교해 보기 위해 그래프를 그립니다.
# legend 값을 확인해 주세요.
df.plot(figsize=(15, 4))
Out[6]:
In [7]:
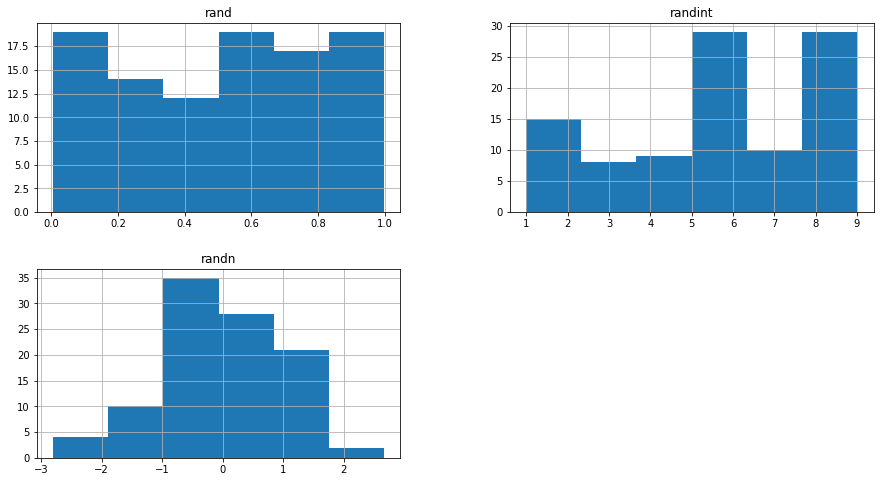
# 같은 값을 히스토그램으로 그립니다.
# rand, randint의 난수생성값에 대해 각 구간의 값의 빈도수를 표현합니다.
# randn은 정규분포(수학자 가우스의 이름을 따서 보통 가우시안 분포라고 부릅니다.) 형태로 난수를 생성한 것을 볼 수 있습니다.
h = df.hist(figsize=(15, 8), bins=6)
In [8]:
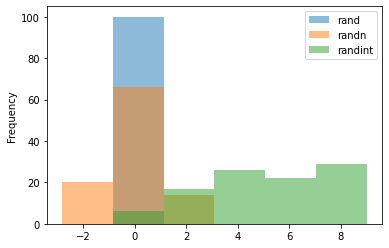
# randn은 다른 분포와 다르게 정규분포 형태의 분포를 생성합니다.
df.plot.hist(alpha=0.5, bins=6)
Out[8]:
In [9]:
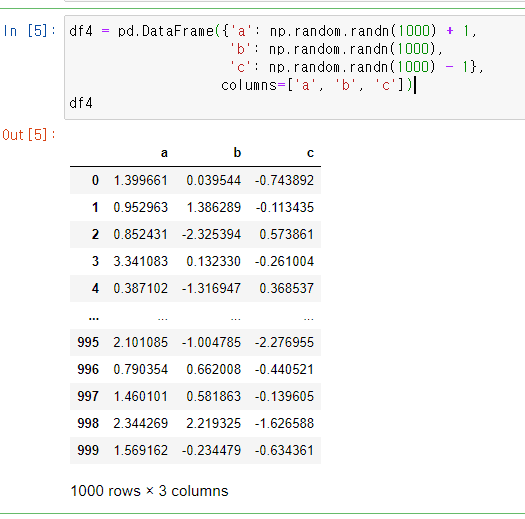
df4 = pd.DataFrame({'a': np.random.randn(1000) + 1,
'b': np.random.randn(1000),
'c': np.random.randn(1000) - 1},
columns=['a', 'b', 'c'])
In [10]:
# 아래에 ... 으로 생략된 값이 나오는데 생략된 값을 모두 보려면
# 아래의 코드의 주석을 풀고 작성해 주시면 최대 1000개의 행까지 보입니다.
# pd.options.display.max_rows=1000
df4
Out[10]:
In [11]:
# 그래프에서 이 값은 -4에서 4까지의 값을 랜덤하게 생성한 것을 확인해 볼 수 있는데요.(좀 더 정확하게 bin 값의 범위입니다.)
# 정규분포의 정의는 평균이 0 분산이 1로 구해지게 됩니다.
# a, c는 1을 빼고 더했기 때문에 평균과 분산이 다르게 나왔는데요.
# b 컬럼은 평균이 0에 가깝고 분산이 1에 가까운 것을 확인해 보실 수 있습니다.
# randn은 rand(랜덤) n(normal) 정규분포값을 생성합니다.
df4.describe()
Out[11]:
In [12]:
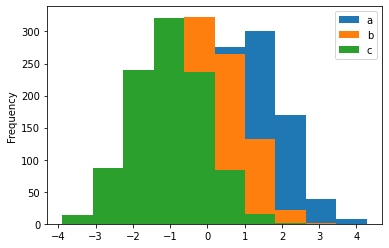
# 아래의 그래프에서 정규분포값을 평균이 0, 분산이 1에 가까운 분포값을 생성해서 히스토그램을 그렸다고 보시면 됩니다.
df4.plot.hist()
Out[12]:
1
0