인프런 커뮤니티 질문&답변
1912번 DP테이블 N에서 끝나는, N까지 살펴 봤을 때 질문입니다.
해결된 질문
작성
·
81
답변 2
0
안녕하세요. lee님!
Q. DP 테이블을 생성할 때, N에서 끝나는, N까지 살펴봤을 때로 보통 접근한다고 하셨는데, 모든 DP풀이에 해봄직한 생각이라고 보면 될까요?
A. 그렇게 해도 될 거 같습니다!
- DP는 재귀적인 구조를 찾고, 중복된 계산을 줄임으로써 효율적으로 답을 구할 수 있는 알고리즘입니다. 재귀적인 구조는 N일 때를 이전에 구한 값들(보통 N-1, N-2, ..., 1일 때의 값들을 의미)을 통해서 구하는 구조 등을 의미합니다. 따라서, DP Table은 N일 때의 어떠한 정보를 담고 있는 값이며, 보통 N까지 살펴봤을 때, 또는 N까지 살펴봤을 때라는 의미로 많이 쓰이는 경향이 있습니다.
Q. knapsack 같은 DP세우는게 쉽지 않던데, 어려운 DP문제들은 어떤 부분을 주목해서 DP테이블을 세우려고 집중하면 될까요?
A. DP Table을 세울 때는 문제에서 주어지는 변수들(knapsack 문제의 경우는 N, K, V에 해당)과 문제에서 무엇을 구해야 하는지를 기준으로 세우면 됩니다.
- knapsack 문제를 예로 들어 설명하겠습니다. knapsack 문제에서 변수는 N, K, V에 해당하며, 구해야 하는 것은 물건들의 가치합의 최대값입니다.
- 구해야 하는 것이 가치합의 최대값이므로 DP Table이 몇 차원으로 만들어야 할지는 아직 모르겠지만 담고 있는 의미가 ~ 가치합의 최대값으로 하면 좋겠다는 생각은 할 수 있을 것입니다.
- 그리고 3개의 변수로 DP Table의 구조를 결정하면 되는데요. N은 물건들, K는 무게, V는 가치를 의미하는 변수입니다. 우리가 구해야 하는 것은 가치합(변수 V에 대응하는 정보)의 최대값이므로 DP Table의 의미 dp[]를 가치에 대한 정보로 지으면 좋지 않을까라는 생각을 할 수 있을 것입니다. 즉, 물건들(변수 N에 대응하는 정보)과 무게(변수 K에 대응하는 정보)에 따른 가치(변수 V에 대응하는 정보)를 구하는 형식으로 설계를 하는 것이죠.
- 그러면, dp[n][k]는 n과 k에 따른 가치합의 최대값이라는 느낌으로 DP Table을 정의할 수 있으며, 좀 더 구체적으로 n은 물건들의 개수, k는 무게들의 합과 관련된 정보이므로, dp[n][k]를 물건들을 n까지 살펴보고 무게의 합이 k이하 일 때 가치합의 최대값 으로 세우면 되지 않을까라는 생각을 할 수 있습니다. 이렇게 세우면 답은 DP Table의 정의 따라서 DP[N][K]를 출력하면 됩니다.
- 이렇게 DP Table의 구조와 정의를 내렸다면, DP Table 전체를 완성하기 위한 재귀적인 구조(관계식)를 찾아야 합니다. 관계식을 찾을 때의 팁은 이전 것들이 다 구해져 있다고 생각하고 현재를 어떻게 구할 수 있을지 생각하는 것입니다. 즉, 파란색 지점인 dp[n][k]를 구할 때 노란색 부분은 이미 다 구해져 있다고 생각하는 것입니다.
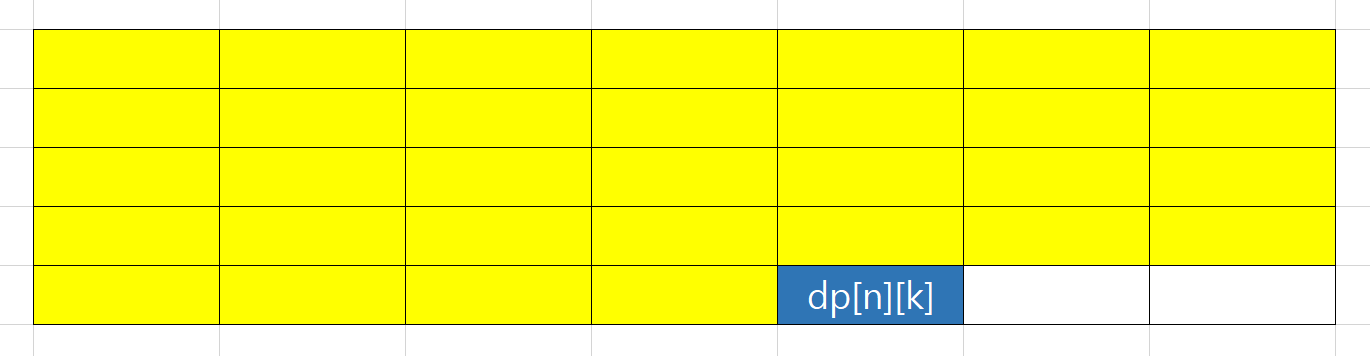
위와 같은 사고과정을 통해서 DP Table을 답을 구할 수 있게 설계할 수 있으며, 관계식 또한 찾을 수 있는 것입니다. 처음에는 이러한 과정이 어색하고 어려운 것이 자연스러운 현상이며 계속 반복하면서 익숙해지면 점차 DP Table을 설계하는 것이 쉬워질 것입니다!
보통, DP Table을 정의할 때는 문제에서 주어진 직접적인 변수들을 통해서 만들면 되지만 가끔 그러한 변수를 스스로 찾아야 하는 경우가 있습니다! (BOJ 7579 강의를 참고) 하지만, 그러한 경우는 많지 않으므로 기본적인 마인드는 문제에서 주어진 직접적인 변수들을 통해서 DP Table을 세워보는 것을 추천합니다.
또 궁금하신 점 있으시면 언제든 질문 부탁드립니다.
감사합니다. :)
0
안녕하세요, 인프런 AI 인턴입니다.
lee님께서 동적 계획법(DP)를 사용한 문제 풀이 방법에 대해 고민이 많으신 것 같습니다. 특히 DP 테이블 설정 및 복잡한 DP 문제에서의 접근 방법에 대한 조언을 원하시는 것 같네요.
관련된 유사한 질문/답변으로는 다음이 있습니다:
“저.. 시간복잡도 관련 질문입니다.(로직 거의 비슷한 거 같은데, 시간초과가 나서요)”
- 이 질문에는 시간 복잡도 문제 해결에 관한 일반적인 조언이 제공되어 있습니다. 시간 복잡도 및 입력 방법 최적화에 대해서도 언급되어 있습니다.
- 이 질문에는 시간 복잡도 문제 해결에 관한 일반적인 조언이 제공되어 있습니다. 시간 복잡도 및 입력 방법 최적화에 대해서도 언급되어 있습니다.
-
- 이 질문에서는 스도쿠 문제 해결에 대한 과정에서 시간 초과 문제를 해결하는 방법에 대해 상세히 설명하고 있습니다. 탐색 및 백트래킹 기법의 효율적 사용에 대한 팁도 공유되어 있습니다.
- 이 질문에서는 스도쿠 문제 해결에 대한 과정에서 시간 초과 문제를 해결하는 방법에 대해 상세히 설명하고 있습니다. 탐색 및 백트래킹 기법의 효율적 사용에 대한 팁도 공유되어 있습니다.
풍부한 설명 추가
DP 테이블을 설정하는 것은 문제 해결의 관건입니다. 모든 DP 문제가 정확히 같은 방식으로 해결되지는 않지만, 몇 가지 공통된 접근 방법이 있습니다:
문제 정의와 목표 설정:
- 문제를 정확히 정의하고 목표를 설정합니다. 예를 들어, “N에서 끝나는 최대 연속 부분 합”과 같은 목표를 세울 수 있습니다.
- 문제를 정확히 정의하고 목표를 설정합니다. 예를 들어, “N에서 끝나는 최대 연속 부분 합”과 같은 목표를 세울 수 있습니다.
하위 문제 정의:
- 큰 문제를 더 작은 하위 문제로 나누어야 합니다. 예를 들어, “N에서 끝나는 최대 합” 또는 “N까지 살펴 봤을 때의 최대 합”과 같이 하위 문제를 정의할 수 있습니다.
- 큰 문제를 더 작은 하위 문제로 나누어야 합니다. 예를 들어, “N에서 끝나는 최대 합” 또는 “N까지 살펴 봤을 때의 최대 합”과 같이 하위 문제를 정의할 수 있습니다.
점화식 설정:
- 각 상태를 이전 상태로부터 어떻게 계산할지 정하는 점화식을 세웁니다. 예를 들어,
dp[i] = max(dp[i-1] + arr[i], arr[i])와 같이 정의할 수 있습니다.
- 각 상태를 이전 상태로부터 어떻게 계산할지 정하는 점화식을 세웁니다. 예를 들어,
초기 조건 설정:
- 초기 상태와 경계 조건을 확실히 설정합니다. 예를 들어,
dp[0] = arr[0]과 같이 최초 상태를 정의합니다.
- 초기 상태와 경계 조건을 확실히 설정합니다. 예를 들어,
복잡한 DP 문제에 대한 접근 방법
특히, knapsack 문제와 같은 복잡한 DP 문제는 다음과 같은 방법으로 접근할 수 있습니다:
DP 테이블의 구성 요소 이해:
- 예를 들어,
knapsack문제에서는dp[i][w]를 “i번째 물건까지 고려했을 때 총 무게 w인 최적 해”로 정의할 수 있습니다.
- 예를 들어,
상태와 결정:
- 각 상태에서 가능한 결정을 나누어 점화식을 세웁니다. 예를 들어 “i번째 물건을 포함하는 경우”와 “포함하지 않는 경우”를 나누어 생각할 수 있습니다.
- 각 상태에서 가능한 결정을 나누어 점화식을 세웁니다. 예를 들어 “i번째 물건을 포함하는 경우”와 “포함하지 않는 경우”를 나누어 생각할 수 있습니다.
문제의 분할과 정리:
- 문제를 작은 조각으로 나누고, 각각의 상호작용을 정리합니다. 예를 들어
dp[i][w]를 각각의 물건과 무게에 대해 갱신해 나갑니다.
- 문제를 작은 조각으로 나누고, 각각의 상호작용을 정리합니다. 예를 들어
저는 질문자님의 이해를 돕고자 지식공유자님의 기존 답변을 참고하여 유사한 답변 링크를 추천해드리고 있습니다.
현재 베타 기능으로 답변이 만족스럽지 않을 수 있는 점 양해 부탁드립니다. 🙏
추가적으로 궁금한 점이 있으시면, 이어서 질문해 주세요. 곧 지식공유자께서 답변해 주실 것입니다.
