인프런 커뮤니티 질문&답변
dp테이블과 tsp의 의미
작성
·
71
0
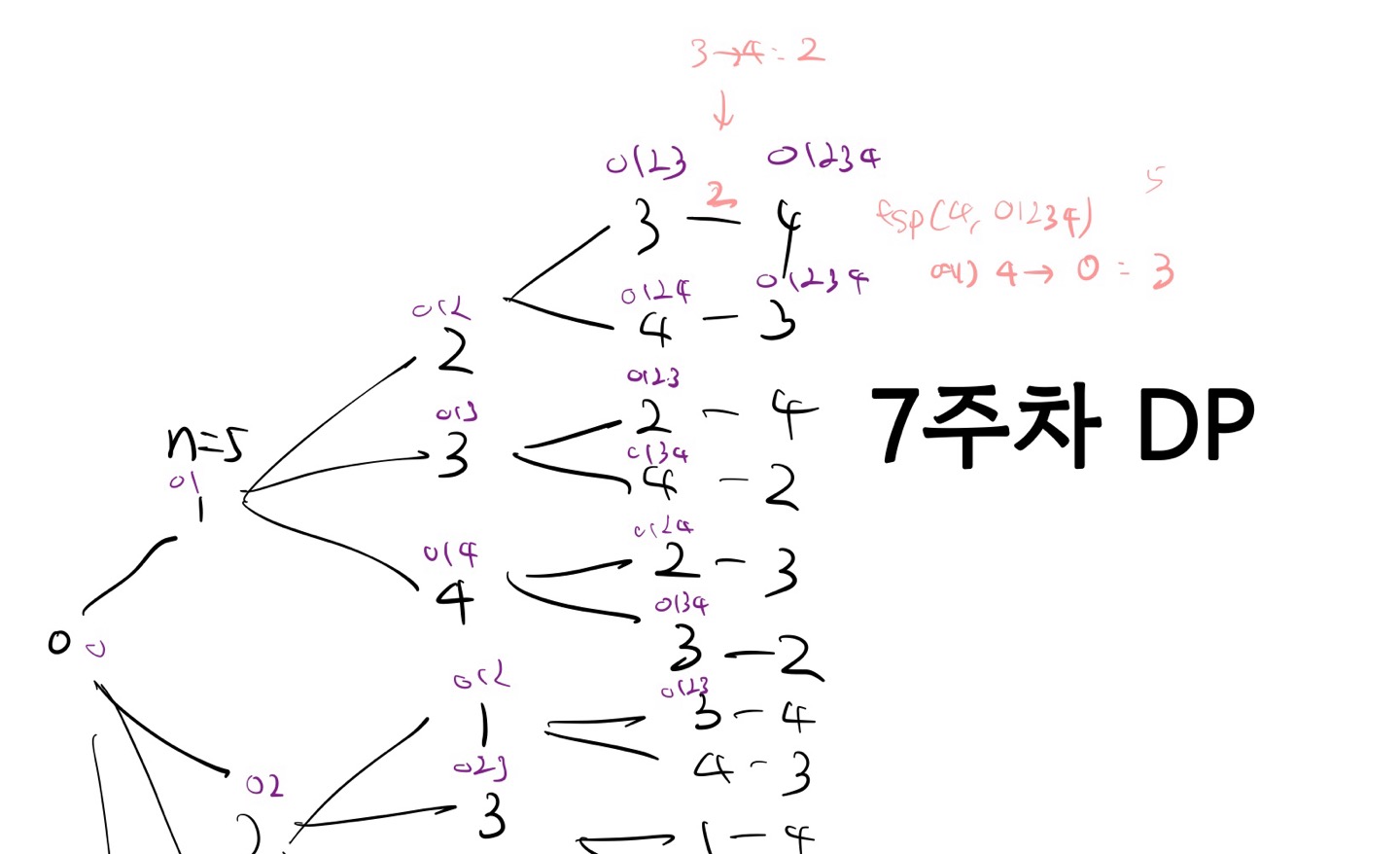
제가 n=5일때 대략적인 코드 흐름을 작성했습니다. 보라색으로 적은 것이 지금까지 방문한 지점(visited를 더 보기 쉽게 표현)입니다.
맨 처음 줄에서 0->1->2->3->4 순으로 방문을 할 때 3->4 에서 tsp가 호출이 되면 tsp(4,01234) 로 호출이 되는데( visited|(1<<i)) 부분을 보기 쉽게 방문한 정점으로 표시한것입니다 ) 4->0으로 가는 weight가 2, 3->4 로가는 weight가 3이라고 가정 하면 tsp(4,01234)는 2를 반환하고 dp[3][0123]=tsp(4,01234)+ (3->4로 가는 weiht) = 2+3 =5가 저장이 되게 됩니다. 그러면 여기서 dp 테이블의 의미는 3에서 부터 시작해서 visited 되지 않은 정점들을 모두 방문하는 최적의 비용을 저장하는게 아닌가요?? tsp도 마찬가지로 here에서 출발해서 visited 되지 않은 정점들 모두 방문하는 방법 중의 최적의 비용을 리턴한다고 생각이 드는데 큰돌 강사님께서 설명하신 부분과 반대로 해석되는거 같아서 여쭤봅니다! ㅜ
그리고 dp에 대해 질문이 있습니다. 제가 이해한 바로는 완전 탐색을 하는데 너무 경우의 수가 많아 중간 중간 예전에 계산해둔 값(dp테이블 등을 이용)으로 중복된 계산을 피해 시간복잡도를 줄이는 것으로 이해했습니다. 그렇다면 이번 문제는 원래는 모든 경우의 수가 16! 절대 완탐으로 풀 수 없어서 dp 방법을 사용하는데 dp를 사용했을 때 이렇게 재귀 함수로 풀면 대략적인 시간복잡도는 계산 못하는 건가요? 보통 문제를 풀기 전에 대략적인 시간복잡도를 측정을 하고 로직을 짜기 시작하는데 이렇게 재귀함수가 들어가고 중간에 dp 테이블을 통해 중복된 계산을 피하는 로직으로 짜면 시간복잡도를 정확히 몰라 뭔가 함부로 시도를 못할거같네요 ㅠ
답변 2
0
안녕하세요 재현님 ㅎㅎ
그러면 여기서 dp 테이블의 의미는 3에서 부터 시작해서 visited 되지 않은 정점들을 모두 방문하는 최적의 비용을 저장하는게 아닌가요??
>>네 맞습니다. dp[here][visited]는 현재 here에 위치하고 있고, visited에 나타난 도시들을 방문한 상태에서, 남은 도시들을 모두 방문하고 시작점으로 돌아오는 최소 비용을 의미합니다.
+ 제가 해당 강의를 봤을 때는 이상이 없었는데요 ㅎㅎ 혹시 어떤 부분에서 제가 반대로 설명했다고 생각하시나요?
그렇다면 이번 문제는 원래는 모든 경우의 수가 16! 절대 완탐으로 풀 수 없어서 dp 방법을 사용하는데 dp를 사용했을 때 이렇게 재귀 함수로 풀면 대략적인 시간복잡도는 계산 못하는 건가요?
>> 보통 DP의 시간복잡도는 DP배열의 최대크기다. 라고 생각하시면 됩니다.
계산 -> 어차피 메모이제이션으로 -> 배열에다가 담고 -> 이정점은 다시방문x 니까요. 이 문제의 경우 n * 2^n이라고 보시면 됩니다.
또 질문 있으시면 언제든지 질문 부탁드립니다.
좋은 수강평과 별점 5점은 제게 큰 힘이 됩니다. :)
감사합니다.
강사 큰돌 올림.
0
안녕하세요, 인프런 AI 인턴입니다.
n=5일 때의 dp테이블과 tsp(TSP, Traveling Salesman Problem)에 대한 설명입니다.
먼저, dp테이블의 의미는 분석하신 것처럼 특정 정점에서 출발하여 방문하지 않은 모든 정점들을 방문하는 최적의 비용을 저장합니다. 여기서 ‘최적의 비용’이란 가장 적은 비용으로 모든 정점을 순회하는 경로를 의미합니다. 따라서 dp[3][0123]가 5가 저장되는 것은, 정점 3에서 시작해 [0,1,2,3]을 방문했을 때, 남은 정점을 방문하고 다시 출발점으로 돌아가는 최소 비용이 5라는 의미입니다.
tsp 함수에 대해서도 정확히 이해하신 것 같습니다. tsp 함수는 현재 위치(here)에서 출발하여 방문하지 않은 모든 정점들을 방문하는 방법 중 최적의 비용을 반환합니다. 여기서 “방문하지 않은 모든 정점”이라는 점이 중요한데, 이는 현재 방문한 정점들을 제외한 나머지 정점들에 대해 최적의 순회를 구하는 것을 의미합니다.
dp를 사용하는 주된 이유는 말씀하신 것처럼 중복 계산을 피함으로써 시간 복잡도를 줄이는데 있습니다. TSP 문제는 모든 경우의 수를 탐색하는 경우 시간 복잡도가 팩토리얼(factrorial)로 증가하기 때문에 완전 탐색으로 모든 경우를 탐색하는 것은 계산상 불가능합니다. 그래서 dp 테이블을 사용해 이미 계산된 결과를 재사용함으로써 계산량을 크게 줄입니다.
재귀 함수로 구현된 TSP 문제에서 dp를 통해 중복 계산을 피하면, 대략적인 시간 복잡도를 계산할 수 있습니다. TSP의 경우 dp 테이블의 크기가 2^n * n입니다(n은 정점의 수). 각 정점에서 출발해 모든 경우를 고려해보는 것을 2^n으로 보고, 각 경우에 대해 n개의 다음 정점을 고려할 수 있기 때문입니다. 따라서 TSP의 대략적인 시간 복잡도는 O(n^2 * 2^n)으로 볼 수 있습니다. 이렇게 dp를 사용하므로써, 비록 재귀 함수가 중첩되더라도 계산이 가능한 범위 내에서 문제를 풀 수 있게 됩니다.
님의 이해가 매우 정확하며, 복잡도를 사전에 파악하는 것이 문제를 풀어나가는 데 중요한 접근 방식 중 하나입니다. TSP와 같은 문제에서는 dp를 통해 중복 계산을 줄임으로써 실제로 구현 가능한 알고리즘을 설계할 수 있습니다.

1:50 쯤 설명에서 {a,b,c}에서 d로 갈때 a,b,c를 방문하는 것 중 최솟값을 찾고 d를 간다고 설명하신 부분때문에 dp[here][visited] 배열에서 만약 visited가 a,b,c 를 방문 표시한 십진수라고 하면 here에서 시작해서 a,b,c를 방문하는 것 중 최솟값을 저장하는 것으로 잘못이해한거 같습니다! 1분 50초 영상에서 헷갈렸던거 같습니다!
직접 문제를 풀어도 큰돌님 해설을 보면서 효율적인 코드가 뭔가 분석하고 제가 만든 코드가 어느 부분이 비효율적인지 알 수 있어 너무 만족하면서 듣고 있습니다! 완전히 이해하였고 답변 감사드립니다!