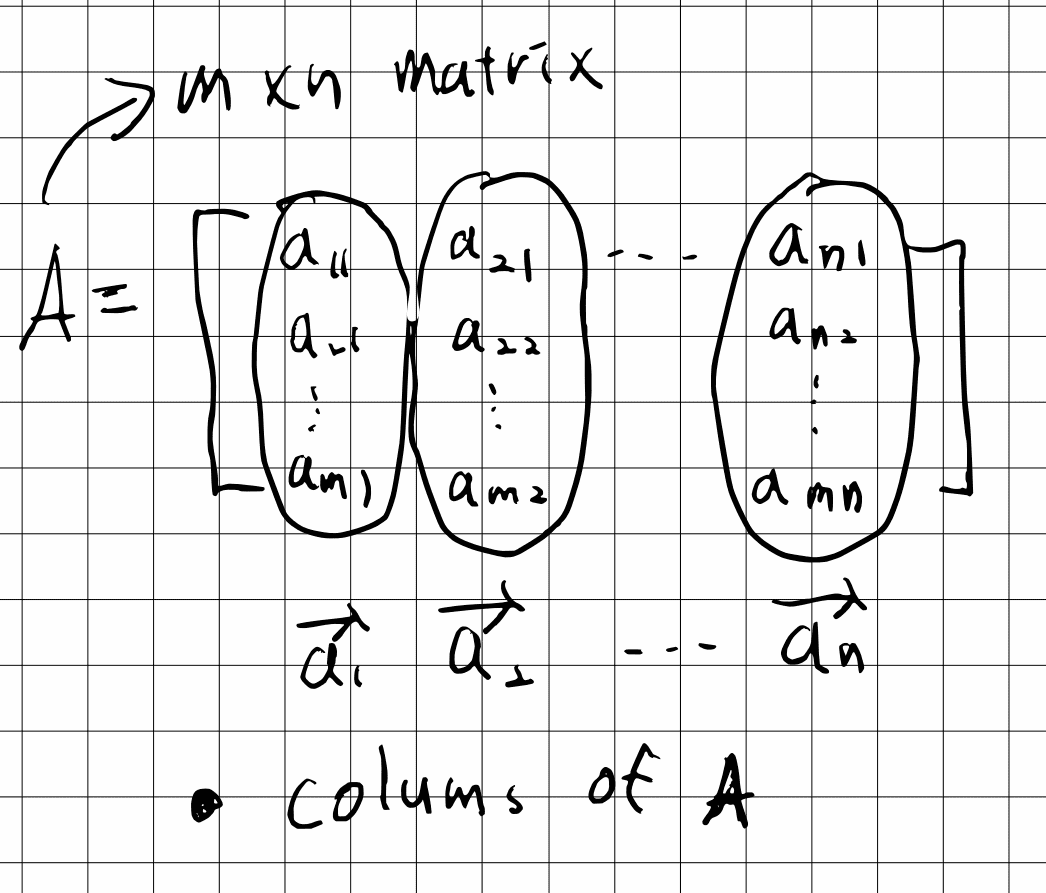인프런 커뮤니티 질문&답변
안녕하세요? 1.4절 듣다가 질문있어서 질문드립니다.
19.09.10 18:21 작성
·
180
1
02:33분경
The matrix equations Ax=b를 설명하는 과정에서
A = [a1, ... , an] [X1 = x1a1 + x2a2 + ... + xnan 이고
...
Xn]
the linear combination of <the columns of A> 라는 내용이 나오는 데
Q1) Column은 세로줄 이고 따라서 위의 식에서 X를 나타내어준 것의 형태여야 한다고 생각하는 데 왜 column이라 명하였는 지 궁금합니다.
Q2) X는 변수로써 작용하는 걸로 이해하고 있습니다. 사실 이건 제가 아직 weights라는 개념에 대해 혼동되어서 질문드리는 데요. 처음 1-3강에서 weights를 설명해주셨을 때 '계수'의 의미인가 했는 데 그건 아닌 거 같더라구요. weights는 그냥 변수로 이해하면 될까요?
답변 3
1
2019. 09. 12. 17:37
b를 A column들의 linear combination으로 표현하기위해서 그리 표현했다라고 생각하면 되실것 같습니다.
A가 m by n이라면 a1부터 an column (vector)들은, 말씀하신것처럼 각 column의 총 entry는 m개입니다.
강좌를 듣다보면 나중에 알게되겠지만 A = [a1 ... an] 처럼 column들로 표현한 경우와 A = (a1,..., am) 의 row 들로 표현한 경우도 발견하게 될것입니다. 어찌됐건 지금처럼 a1부터 an을 column으로 표현한 경우 각 column의 entry가 몇개인지 그리고 A matrix의 모양과의 비교를 통해서 상황들을 명확히 이해하고 있으면 됩니다.
간단히 생략하기 위해 위와같은 형태로 써도 무관하지만, 지금은 column 들의 linear combination의 관점을 표현하기위한것이 더 크다라고 생각하시면 됩니다. 그리고 Ax의 정의 (product of A and x)가 본래 A column들의 x entry를 통한 a1*x1+...+an*xn형태의 linear combination이라는 점도 잊으시면 안될 것 같고요.
=====수정됨 (2019.09.14)====
뒷부분 질문은 동영상을 확인해보니 A가 Rm space에 있다라고 말한것이 아니라, a1부터 an까지 들이 Rm space에 있다라고 말한것입니다. 한번 다시 천천히 확인해주세요 ㅎ
=============
감사합니다.
1
2019. 09. 10. 18:41
Q1)
노트에 적어봤습니다. a1부터 an까지는 A의 column들이라는걸 바로 이해하실수 있을겁니다.
x1부터 xn을 "coefficient"들이라 생각하면 a1 x1+...+an xn 은 A column들의 linear combination이라는 점이 명확해 질겁니다.
Q2)
보는 관점에 따라 다릅니다.
예를들어, Ax = b의 matrix equation에서 x의 solution을 구하고자 하는 경우라면 x는 unknown들, 미지수라고 볼 수 있을겁니다. 이 경우 변수로 생각할 수 있을겁니다.
이미 해를 알고 있는 상황이라고 해봅시다.
그 경우엔 b를 이해하는데 있어서 A의 column들에 붙는 coefficient들로 생각할 수 있을 겁니다.
답변이 부족하다면 질문을 추가로 해주세요ㅎㅎ
감사합니다.
0
2019. 09. 12. 17:13
우선 친절한 답변 너무 감사합니다.
Q1)에서 조금더 덧대어 질문드리고싶은데요.
A = [a1, ... , an] / A 행렬을 이렇게 표현한 것은 원래 a1열에는 a11~am1까지 있는 데 그것이 생략된 형태라고 봐야할까요? 아니면 a1의 벡터가 a11~am1을 다 포함하고 있어서 굳이 길게 표현안하고 그냥 a1을 벡터의관점에서 a1이라고 쓴 것인가요?
그리고 1.4절에서
A = [a1, ... , an] [X1 = x1a1 + x2a2 + ... + xnan 이고 x1a1 + ... + xnan 이 R^m SPACE에 있다고 하시고
... A가 원래 R^m 스페이스에 있다고 하셨는 데 A가 원래 m x n 행렬인데 왜 A가 R^m space인지 모르겠습니다ㅠ
Xn]